05.12.2014
Parametrisches Modell 4
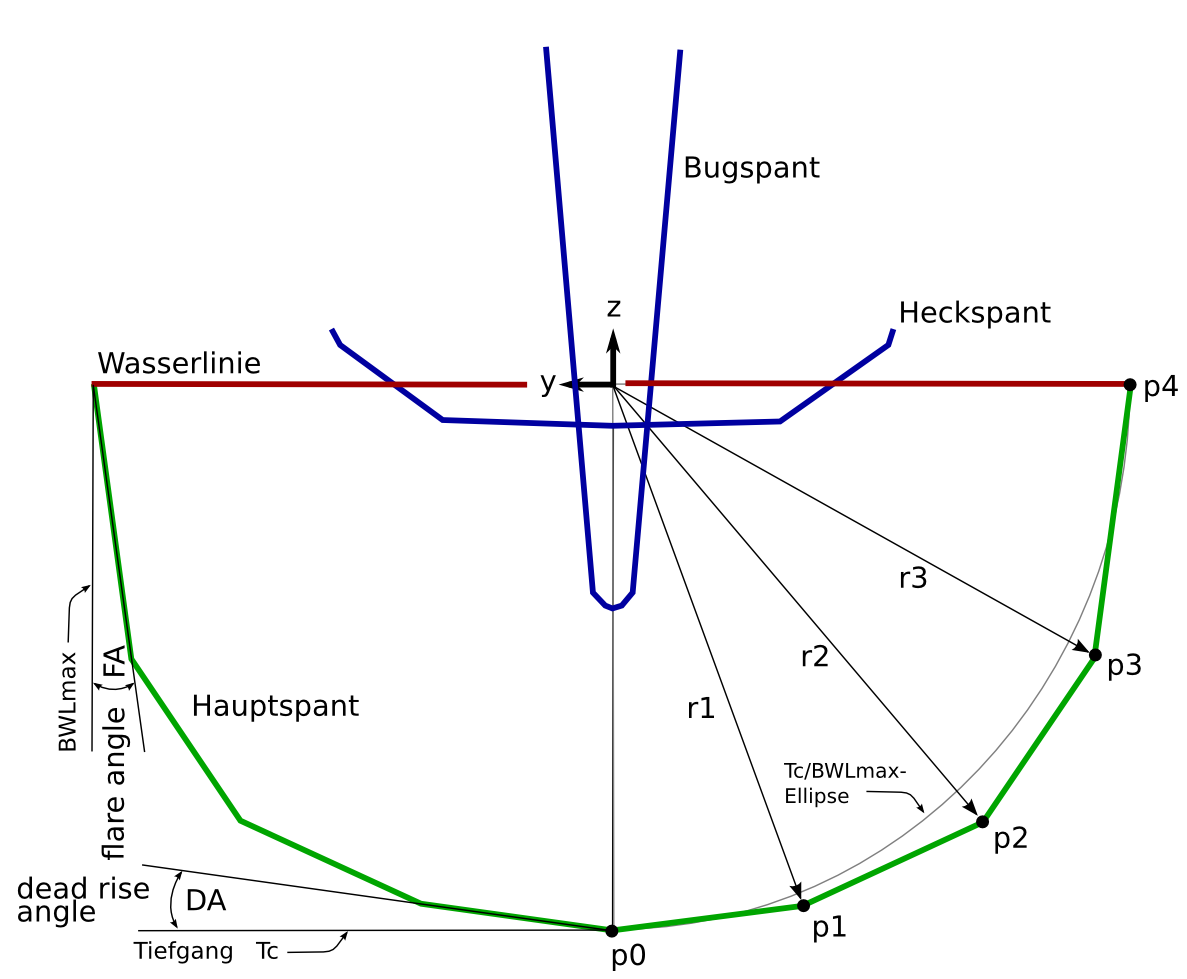
Abbildung 1: Geometrie des Modells 4a
Modell 4 ist aus der Idee entstanden, dass man mit einem Knick mehr im Unterwasserschiff die durch Tc und BWL aufgespannte Ellipse besser annähern kann und dadurch die benetzte Fläche reduzieren kann. Allerdings erwies es sich als schwierig, in diesem Fall die Kantenlänge des Spants im Unterwasserberich tatsächlich zu minimieren, weil die Spantfläche in diesem Modell nicht direkt als Parameter eingeht. Optimierungsversuche von Hand haben ergeben, dass eine Reduktion der benetzten Fläche so nicht möglich ist. Bei den guten Designs bewegt sie sich immer im Berich von 46,0 bis 46,3 m² pro Rumpf, egal, ob zwei oder drei Knicke im Unterwasserschiff vorhanden sind. Allerdings führte der zusätzliche Knick zu einer besseren Lage des Auftriebsschwerpunktes (XCB) im Vergleich zu zum Wasserflächenschwerpunkt (XCF): XCB is etwas nach hinten gewandert, was im Hinblick auf die generelle Hecklastigkeit moderner Fahrtenkatamarane vorteilhaft ist. Da aber XCF nicht auswandert, das die Wasserlinie unverändert geblieben ist, liegen beide nun dichter beisammen, was theoretisch zumindest das Seegangsverhalten verbessert. Der zusätzliche Knick bietet also durchaus Vorteile bei den Kennwerten.
Bestimmen der Spantflächengeometrie
Eine geschlossene Lösung unter Vorgabe der Spantfläche konnte ich hier nicht finden.
Daher sind die Parameter in diesem Modell der dead rise angle (DA), flare angle (FA), die
wie im Modell 3 definiert sind. Zusätzlich werden noch Tc und BWL als Eingabewerte
benutzt. Allerdings werden diese Werte im Vorfeld über die designtechnisch wichtigere
Größe der Breiten-Tiefgangs-Ratio
$BTR = {BWL \over T_c}$ miteinander verknüpft.
Die Lage der Punkte p1 und p3 wird über den Satz des Thales bestimmt, wobei die Radien
r1 und r3 in Anlehnung an Tc bzw. BWL vorgegeben werden, und zwar so, dass sie die
Ellipse gut annähern. Der Punkt p2 wurde mittig zwischen p1 und p3 auf einer Kreislinie
mit dem Radius r3 positioniert. Dieser Radius wurde experimentell so gewählt, dass
man ein günstiges Verhältnis von Spantkantenlänge und Spantfläche bekommt. Wie man
in Abbildung 1 sieht, wandert p2 sehr deutlich von der BWL-Tc-Ellipse aus. Meine
Experimente am Computer haben aber ergeben, dass ich damit bessere Ergebnisse erziele,
als wenn die Punkte stur der Ellipsenkurve folgen würden.
Der Vorteil an diesem Verfahren ist natürlich, dass die Spantfläche schneller erzeugt
wird, wenn man sie benutzt, um die Verdrängung auf den Standardwert (zur Zeit 18 Tonnen)
optimiert.
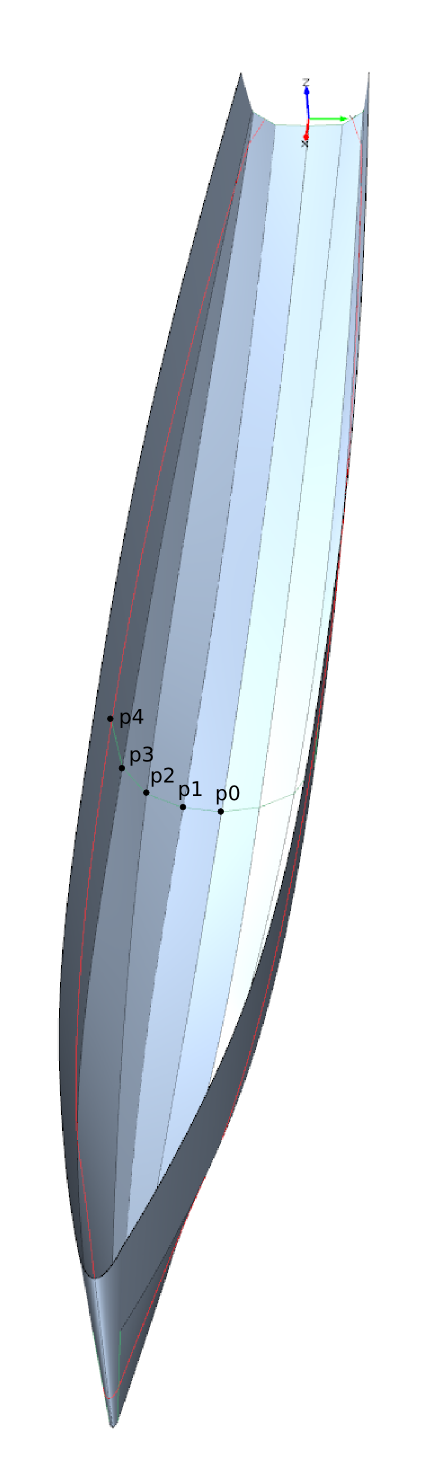
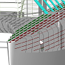
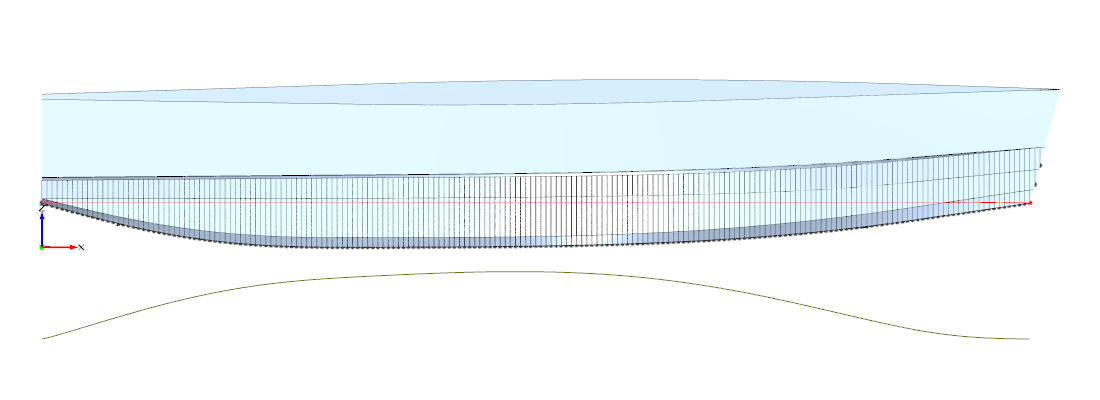
Abbildung 2: Beispiel eines generierten Modells 4a
Modellerweiterungen
Die Bildunterschriften Modell 4a
lassen erahnen, dass das Grundmodell weitere
Verfeinerungen erfahren hat: Die Oberkannte der generierten Spantflächen von Bug und
Heckspant müssen nicht mehr auf der Wasserlinie liegen.
Am Bug führt das dazu, dass ich durch den zusätzlichen Knick einen sehr feinen Bug erzeugen kann, der eine kleinere Bugwelle erzeugt und somit den Wellenwiderstand reduziert. Durch die leicht konkav wirkende Form über der Wasserlinie, sollte auch das über Deck kommende Wasser etwas reduziert werden.
Am Heck ermöglicht diese Trennung einen zusätzlichen Knick durch unterschiedliche flare angles für den Spantbereich und die daran anschließende Verlängerung über der Wasserlinie. Da dieser Winkelunterschied am Hauptspant nicht umgesetzt wird, laufen die Knicklinien sauber durch. Somit erhält der Rumpf über die gesamte Länge 3 Knicklinien im Unterwasserbereich. Das Heck wird dadurch etwas gefälliger, weil runder.
Die ursrüngliche Idee dieser höhenverschiebbaren Heckspanten war es, auch klassische
Yachthecks untersuchen zu können. Diese Idee habe ich aber wieder verworfen, da sie
dem Ziel einer Halbgleiterfahrt entgegenläuft. Darüber hinaus bereitet eine solche
Knofiguration in SHIPFLOW Schwierigkeiten, weil man sich dort im Vorfeld für oder
gegen einen wet transom
Simulation entscheiden muss. Nur leider wird bei höheren
Geschwindigkeit aus dem trockenen ein nasser Spiegel. Durch die Heckspantfläche kann
ich die Position der Knickpunkte direkt beeinflussen: Bei einer größeren Fläche
wandert (geometriebedingt) Hauptsächlich der erste Knick von der Mittschiffslinie
aus gesehen nach außen. Ich werde das nutzen, um zu untersuchen, ob ein breites flaches
Surfbrett
am Heck zu einem geringeren Widerstand bei hohen Geschwindigkeiten
führt.
Parametric High Performance Designs
Angeregt durch den Artikel Rumpfgeschwindigkeit
in dem Palstek 01/15, in dem es
auch um pfh
(parametric high performance) Heckformen geht, habe ich auch dazu kurz
experimentiert. Wenn man die Webseite dazu genau liest, merkt man dass es dabei um echte
Gleitfahrt bei Foudezahlen zwischen 1 und 1.5 geht. Dementsprechend bietet so ein Ansatz
hier keine Vorteile, ließe sich aber in gewissen Grenzen mit meinem Modell abbilden.
Jedenfalls wären solche Untersuchungen, wie auf der pfh Webseite als so genial verkauft werden,
mit dem Friendship-Framework (CAESES) und SHIPFLOW oder einer anderen CFD-Software keine
große Sache. Im Prinzip ist das nichts anderes als das, was ich hier auch mache.
Allerdings verwende ich keine Optimierung im mathematischen Sinne, sondern gezielte
Untersuchungen des Parameterbereichs. Allerdings ist auch das mit dem Framework leicht möglich,
wenn man genug Rechenpower und wenige Parameter hat.