2.ll.mode
Parametrisches Modell 2
Nachdem sich herausgestellt hatte, dass mit dem parametrischen Modell 1 zu wenig direkten Einfluss auf die wichtigen Schiffsparameter wie maximale Breite an der Wasserlinie, maximale Spantfläche, Verdrängung oder Tiefgang möglich ist, musste ein neues Modell her.
Es sollte der große Wurf werden: Inspririert durch die ksplines von Kevin Cudby aus Neuseeland sollte das Modell aus einem Satz Designparameter(kurven) (Mittschiffsline, Wasserflächenline, Spantflächenkurve, Bodenwinkel, Seitenwinkel, ...) eine beliebige Anzahl von Knickspantflächen erzeugen können. Die einzelnen Punkte der Knicke auf den Spanten sollten dann zu einem durchgehenden Knick verbunden werden. Diese Kurven würden dann die Begrenzungslinien für die abwickelbaren Rumpfflächen bilden. Damit sind die Verdrängung, der Verdrängungsschwerpunkt, der Wasserflächenschwerpunkt, der Tiefgang etc. direkt vorgebbar.

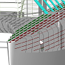
Abbildung 1: Spanten unter Vorgabe des Seitenflächenwinkels (Seitenansicht)

Auf Grundlage meiner vorherigen Designexperimente habe das Unterwasserschiff mit zwei Knicken ausgelegt. Indiesem Fall ist es möglich durch geschickte Wahl der Designparameter(kurven), die Lage der zwei Knickpunkte unter Berücksichtigung aller Designparameter als geschlossenen Ausdruck mit Hilfe einer quadratischen Gleichung zu bestimmen. Um das zu erreichen und damit das System nicht überbestimmt ist, wurde auf den Spantenschwerpunkt als Designparameter verzichtet und stattdessen der Winkel der Mittleren fläche gegen die Waagerechte vorgegeben. Da es sich bei allen Designparametern um Designkurven über die gesamte Schiffslänge handelt, ändern sich die Parameter kontinuierlich über die Schiffslänge.
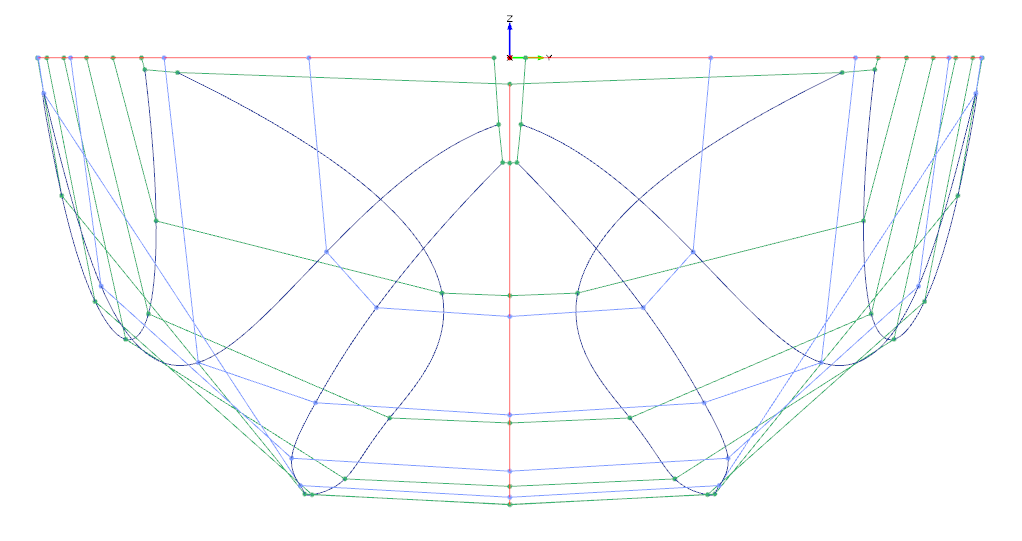
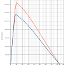
Abbildung 2: wie Abb. 1 (Frontansicht)
Soweit, so gut, doch hat die Sache einen Haken: Verbindet man die Knicke der Spanten über die Schiffslänge, erhält man leider keine glatten Kurven, sondern Schlangenlinien (vgl. Abbildungen 1-4). Selbst wenn man die Designparameter für die Winkel konstant über die Länge hält, verschwinden die Schlangenlinien nicht. Der Zusammenhang zwischen Designparametern und der Lage der Knickpunkte in x-z bildet leider nicht auf eine monoton-konvex gekrümmte Kurve ab. Auch ist es schwierig besonders die Mittschiffslinie, die Wasserlinie und die Spantflächenkurve so zu definieren, dass alle Spantflächen der Spantflächenkurve sich auch auf die von Wasserlinie und Mittschifflinie aufgespannte Geometrie abbilden lassen, d.h. dass man unter Berüchsichtigung aller Parameterkurven eine Spantfläche konstrieren kann, die alle Parameterwerte einhält. In den Abbildungen wurden die Spantkurven farblich gekennzeichnet:
- Grün, wenn alle Parameter erfüllt sind,
- Blau, wenn die Spantfläche unter der Spantflächenkurve an der entsprechenden x-Position der Spantflächenkurve kleiner ist, als die minimal geometrisch erreichbare oder
- Rot, wenn die Spantfläche unter der Spantflächenkurve an der entsprechenden x-Position der Spantflächenkurve größer ist, als die maximal geometrisch erreichbare.
In Abbildung 2 kann man blaue und grüne Spantkurven sehen. Wasserlinie und Mittschiffslinie sind rot dargestellt. Die Knickkurven (Schlangenlienien) in dunkelblau. Die Spantfächenkurve (nur in den Seitenansichten) ist schwarz dargestellt.

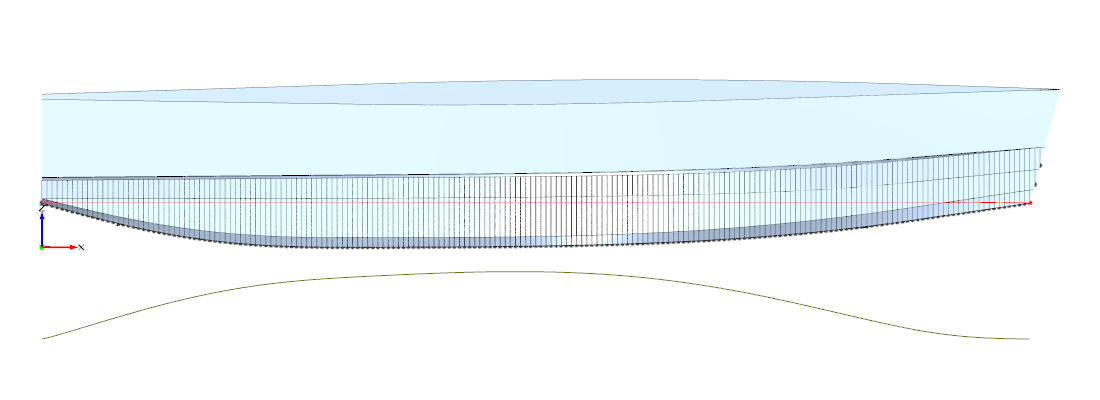
Abbildung 3: Spanten mit minimaler Seitenflächenlänge (Seitenansicht)
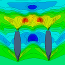
Alternativ habe ich getestet, wie die Knickspanten aussehen, wenn man nicht den Seitenflächenwinkel, sondern eine minimale Gesamtspantkurvenlänge als zusätzlichen Parameter heranzieht. Der Sinn dieses vorgehens liegt auf der Hand: Haben alle Spanten minimale Kantenlängen, ist auch die benetzte Fläche unter berüchsichtigung aller anderen Parameter minimal. Man kann erkennen, dass die Knickkurven in der Seitenansich graduell geradliniger sind, aber nach wie vor alles andere als glatt und strakend.
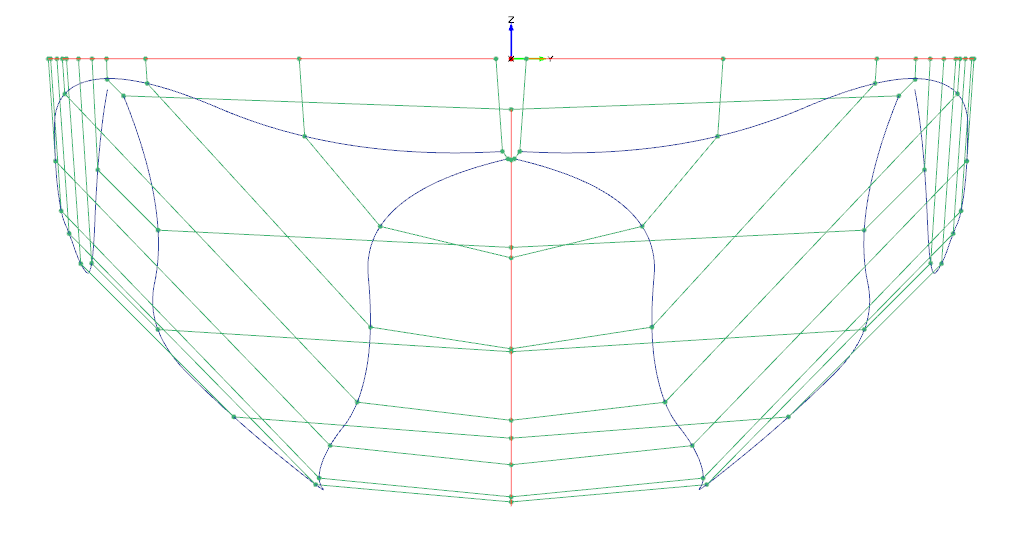
Abbildung 4: wie Abb. 3 (Frontansicht)
Berücksichtigt man dann noch den Aufwand, der erforderlich ist, eine Designkurvenkombination zu finden, so dass alle Parameter für alle Spanten erfüllt werden können, erkennnt man schnell, dass dieses Vorgehen leider in eine Sackgasse führt.
Dennoch hatte diese Exkursion auch etwas Gutes: Es hat sich gezeigt, dass die quadratische Gleichung taugt, um Knickspanten mit definierten Eigenschaften zu generieren. Benutzt man lediglich drei Spanten, einen am Bug, einem am Heck und einen für den Hauptspant und verbindet diese mit Friendships parametrischen Kurven, erhält man immerhin ein Modell, bei dem Tiefgang, maximale Breite an der Wasserline, Hauptspantfläche und Wasserlinenschwerpunkt direkt vorgegeben werden kann. Verdrängung und Verdrängungsschwerpunkt ergeben sich nur als abhängige Größen, lassen sich aber immerhin über die Größe der Hauptspantfläche und deren Position in Schiffslängsrichtung direkt beeinflussen. Das ist definitiv ein großer Fortschritt gegenüber dem parametrischen Modell 1!
Eine weitere Einschränkung besitzt das Modell jedoch: Es ist zwingend, dass der Rumpf einen eingetauchten Heckspiegel hat, da sonst der Heckspant in der Wasserline nicht bestimmbar wäre. Allerdings haben meine Recherchen ergeben, dass dies sowieso das Design der Wahl sein dürfte, weil man dadurch die effektive Wasserlinienlänge vergrößert, sobald die Stömung am Heck sauber abreißt. Auch der Trimwinkel soll dabei kleiner sein, was sich auch positiv auf die Geschwindigkeit auswirkt.