Minimierung der benetzen Fläche - erster Versuch
Um die benetzte Fläche (S) zu minimieren, wurden die Breitenparameter B0, B1 und B2 variiriert. Die Minimierung erfolgt mit einem Nelder-Meads-Simplex-Verfahren. Dabei kann der untersuchte Raum n-dimensional (Breiten B0, B1, B2) sein, allerdings kann das Verfahren in Friendship nur eine Zielgröße (benetzte Fläche S) minimieren. Das ganze ist natürlich nur dann sinnvoll, wenn man das verdrängte Volumen konstant hält. Andernfalls wäre die Lösung trivial (B0, B1, und B2 am unteren Grenzwert) und unbrauchbar. Die einfachste Lösung wäre, wenn man das Volumen als zusätzliche Bedingung fixieren würde. Doch dann würde man überwiegend unbrauchbare Lösungen berechnen, weil das Optimierungsverfahren den Wert zwar als Grenzwertüberschreitung kennzeichnen würde, aber keine Strategie hat, eine solche zu vermeiden.
Deshalb wurde hier das Volumen durch Anpassung des Tiefgangs nachgeführt: Jedesmal, wenn sich die Breiten ändern, nähert ein Newton-Raphson-Minimierer das verdrängte Volumen an das Zielvolumen an, indem es den Tiefgang variiert.

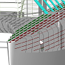
Abbildung 1: Ausgangsdesign

Abbildung 2: Kompromiss, mit L/B=10

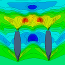
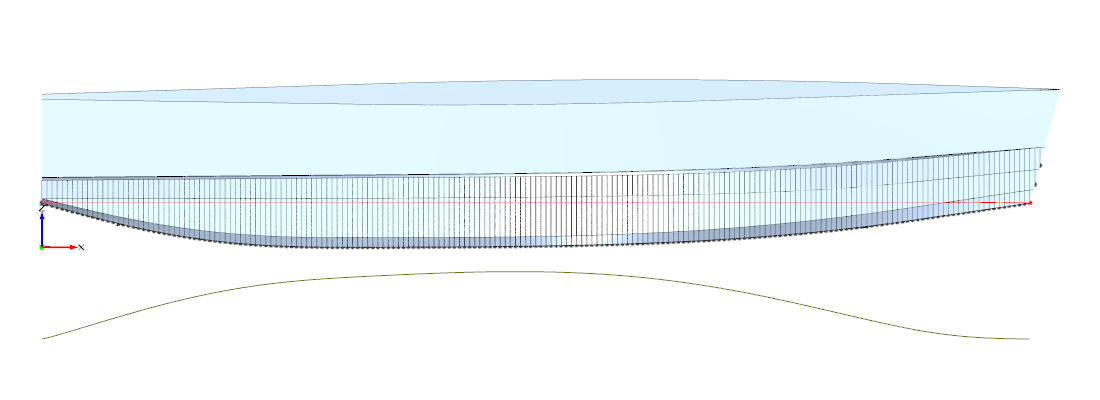
Abbildung 3: Minimale benetzte Fläche
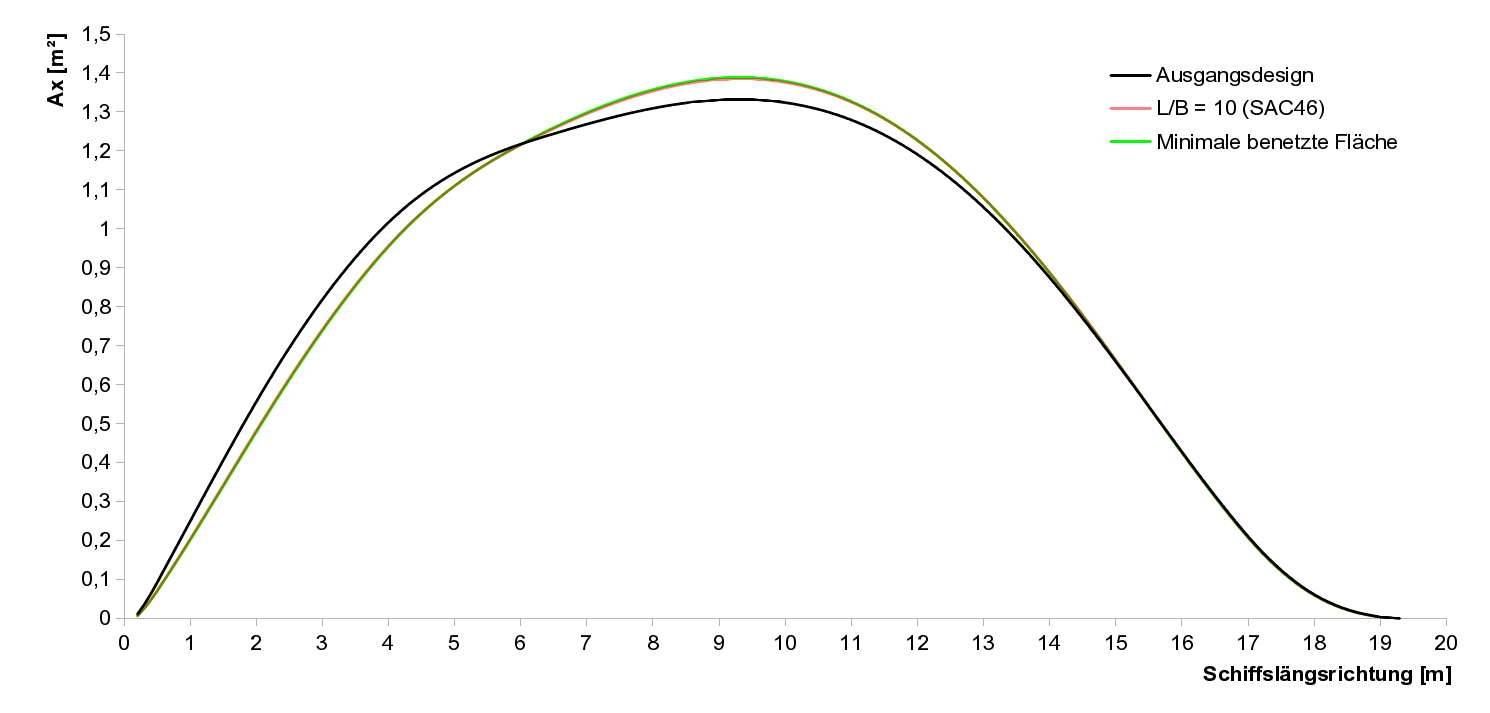
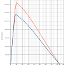
Abbildung 4: Spantflächenkurven der drei Designs
Abbildung 1 zeigt das Ausgangsdesign, dass ich per Hand so weit verändert habe, dass es meinen Ansprüchen an die Hydrostatik genügt. Abbildung 2 zeigt ein Design, bei dem gerade noch ein Längen-/Breitenverhältnis von 1:10 erreicht wird. Das ist nach meinen Literaturrecherchen der Wert unterhalb dessen der Wellenwiderstand stark ansteigt. Ob das so stimmt, müssen die CFD-Simulationen zeigen. Abbildung 3 schließlich zeigt das Design mit minimaler bennetzter Fläche. Abbildung 4 zeigt die Spantflächenkurven in stark überhöhten Maßstab. Man kann man einige Unterschiede in den Spantflächenkurven erkennen: Zum einen natürlich, dass die Maxima der optimierten Rümpf viel höher liegen, aber auch die Formen sind verschieden. Besonderes Augenmerk werde ich auf die Tatsache legen, dass das Ausgangsdesign im Heckbereich einen recht ausgeprägten Knick aufweist. Was für eine Auswirkung hat soetwas auf das Seegangsverhalten? Der Heckbereich ist dadurch recht steil. Erschwert das das Gleiten?
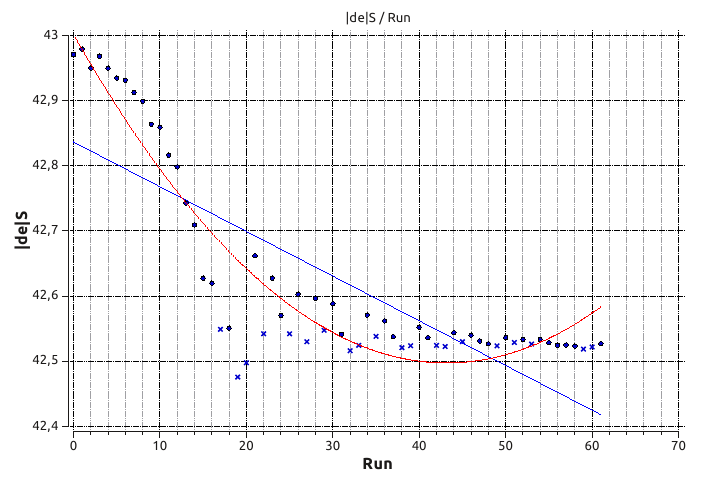
Abbildung 5: Benetzte Fläche (de|S) über die Iterationen
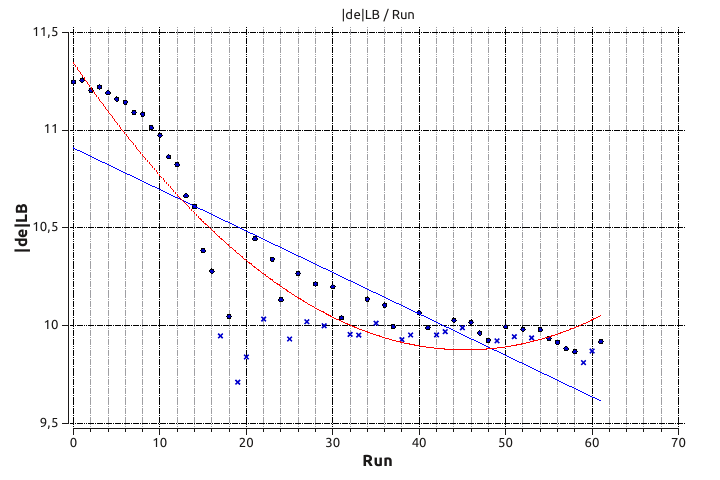
Abbildung 6: Verhältnis L/B (de|LB) über die Iterationen
Die Friendship-Framework-Datei findet sich hier. Wer Lust und Zeit hat, kann sich die gerne einmal ansehen.
Die quantitativen Ergebnisse fallen eher ernüchternd aus: Abbildung 5 zeigt die Abnahme des benetzten Fläche. Diese geht von 42,971 m² auf 42,524 m² zurück. Das entspricht gereade einmal einer Reduktion um 1%. Das Länge-zu-Breite-Verhältnis (L/B) hingegen nimmt von 11,247 um satte 12,3% auf 9,868 ab. Das bedeutet, dass einer marginalen Flächenreduktion ein massiver Verlust von LB-Verhältnis gegenübersteht. Das ist definitiv keine Richtung, in die man die Optimierung weiterttreiben sollte. Auch die weiteren hydrostatischen Werte (vgl. Tabelle 1) zeigen keine unerwartete positive Entwicklung: Der Rumpf wird im ganzen flacher und breiter.
Offenbar wurden hier nicht nicht Haupteinflussfaktoren gewählt oder das Ausgangsdesign war schon recht nahe am Optimum. Vielleicht ist auch einfach das Modell zu rigide und erlaubt zu wenig Variationsmöglichkeiten. Auf jeden Fall sollte ich die Frage untersuchen, woran es liegt, dass die benetzte Fläche so unsensibel auf eine Breitenanpassung reagiert? Darüber hinaus wäre mit Hilfe einer CFD-Untersuchung zu klären, wie stark sich eine breitere/flachere Rumpfform gegenüber einer schmaleren/tieferen auf den Wellenwiderstand auswirkt. Erfahrungsgemäß heißt es, dass etwas tiefere schmalere Designs tendenziell weniger Widerstand bieten.
Ein weiterer Punkt, der mir aufgefallen ist, ist, dass der Rumpf durch die Lage der Knicke des Knickspantdesigns am Bug in der Wasserlinie eine leicht konkonkave Form aufweist. Meiner ersten Einschätzung nach könnte das zu einer vorzeitigen Strömungsablösung führen, aber sicher bin ich mit da nicht. Ich sollte auf jeden Fall ein Alternativdesign aufsetzen, das dieses Problem nicht hat.
| Parameter | DCOne Ausgangs-modell | DCOne Schritt 46 | DCOne Schritt 58 (Smin) |
|---|---|---|---|
| AW Wasserlinienfläche [m²] | 24,249 | 25,964 | 26,276 |
| AX Größte Spantfläche [m²] | 1,332 | 1,385 | 1,389 |
| BWL Größte Breite der Wasserlinie [m] | 1,707 | 1,916 | 1,946 |
| Cb Blockkoeffizient | 0,510 | 0,495 | 0,493 |
| Cm Koeffzient der größten Spantfläche | 0,820 | 0,822 | 0,822 |
| Cp Prismatischer Koeffizient | 0,625 | 0,602 | 0,600 |
| Cw Wasserlinienflächenkoeffizient | 0,740 | 0,706 | 0,703 |
| DISPM Verdrängte Masse (Salzwasser) [t] | 16,399 | 16,399 | 16,399 |
| DISPVOL Verdrängtes Volumen [m3] | 15,999 | 15,999 | 15,999 |
| Draft Tiefgang [m] | 0,940 | 0,871 | 0,860 |
| KML Metazentrische Höhe in Längsrichtung [m] | 32,334 | 33,244 | 33,356 |
| LB Längen/Breitenverhältnis | 11,247 | 10,020 | 9,868 |
| LWL Länge der Wasserlinie [m] | 19,200 | 19,200 | 19,200 |
| S Benetzte Fläche [m²] | 42,971 | 42,540 | 42,524 |
| Tpc Verdrängungszunahme bei 1cm Tiefertauchung [m3] | 0,243 | 0,260 | 0,263 |
| XCB Auftriebsschwerpunkt in Längsrichtung vom Heck [m] | 8,832 | 8,963 | 8,965 |
| XCBp XCB auf LOA (Länge ü. Alles) bezogen [%] | 44,161 | 44,840 | 44,826 |
| XCF Schwerpunkt von AX vom Heck [m] | 9,010 | 9,188 | 9,192 |
| XCFp XCF auf LOA bezogen [%] | 45,052 | 45,942 | 45,958 |