30.08.2015
Entwurf 1

Abbildung 1: Entwurf 1 - 2011
Jeder, der schon einmal ein Haus gebaut hat, weiß, dass den
Architekten oft mehr ihr Geldbeutel als ein optimales Ergebnis für den
Kunden am Herzen liegt. Warum sollte dies beim Schiffbau,
insbesondere beim Yachtbau, anders sein?
Doch wie fängt man mit einem Entwurf an? Zuerst muss man eine
geeignete Entwurfssoftware finden. Wichtigstes Kriterium für mich: Sie
muss
auch mit Katamaranen umgehen können. Das ist leider nicht
selbstverständlich. Meine ersten Entwürfe eines Rumpfes habe ich mit
MaxSurf gemacht, das verspricht, auch mit Katamaranen klarzukommen.
Davon gibt es beim Hersteller eine CrippleWare
-Version zum
Ausprobieren. Die Beschränkung auf drei Flächen ist für ein
Knickspantdesign untragbar. Allerdings war es für mich der richtige
Einstieg, die Grundprinzipien des 3D-Entwurfs zu verstehen.
Auf der CMM 2010 in Hamburg konnte ich zu Friendship-Systems
Kontakt aufnehmen, die ein sehr gutes aber für Anfänger- und
durchschnittliche Hobbybastler
zu komplexes parametrisches
Entwurfs- und
Optimierungssystem anbieten. Die Lernkurve ist sehr steil, aber nach
dem ersten Entwurf einer kompletten Katamaranhülle mit zwei Rümpfen und
Brückendeck hatte ich schon ettliche
Dinge begriffen und konnte mich daran wagen, ein parametrisches Design
von einem Rumpf aufzusetzen.
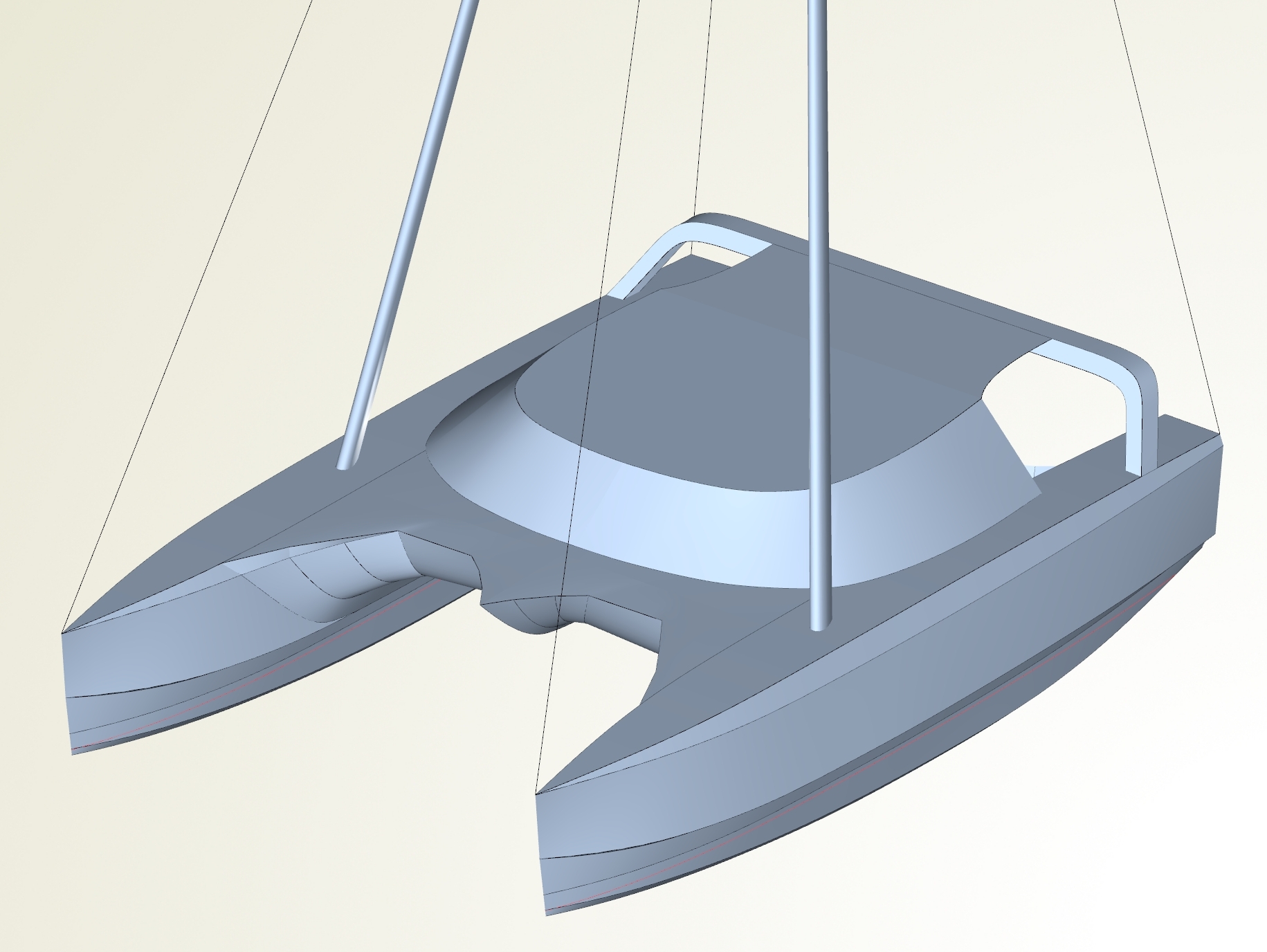
Abbildung 2: DreamcatcherOne-Entwurf 2011
Die um Segel, Mast, Steuerhaus etc. vervollständigte Version meines ersten Entwurfs
habe ich Modell 0 genannt. Es ging darum zu prüfen, ob Das Friendship-Framework, seit
2015 nur noch als CAESES
bekannt, in derLage ist, meine Modellvorstellungen
abbilden zu können. Wie sich im Nachhinein herausgestellt hat, habe ich mit CAESES eine
sehr gute Wahl getroffen, da das Programm seit 2010 rasant weiterentwickelt worden ist.
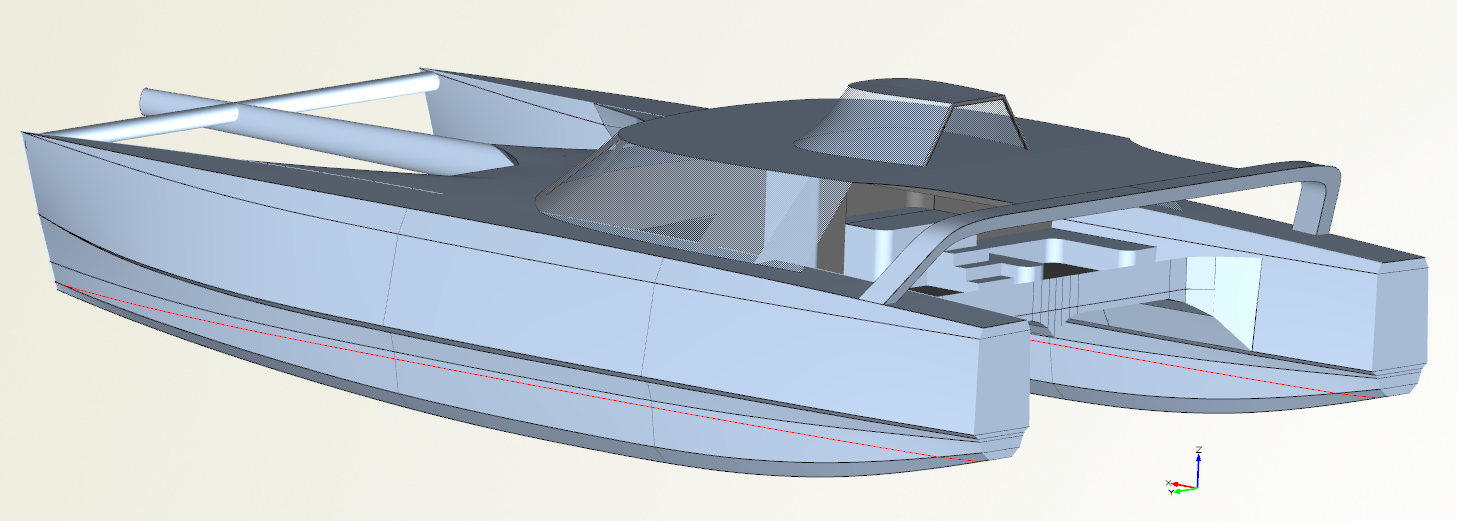
Abbildung 3: Modell 0 ohne Segel (2013)
Die Schwimmer dieses Ausgangsmodells sind nicht parametrisiert und beruhen auf BSpline-Kurven, wie man das auch mit einem handelsüblichen Schiffsdesignprogramm machen würde. Der Nachteil dieser Herangehensweise ist, dass es mit vertretbarem Aufwand nicht möglich ist exakt strakende Linien zu zeichnen. Will man dann noch Krümmungskontinuität (C2-Kontinuität, 2. Ableitung hat keine Knicke) kann man diesen Ansatz getrost als nicht durchführbar ansehen.
Allerdings sind die Maße in Querrichtung parametrisiert, so dass sich ein Design beliebiger Breite erzeugen lässt. Nach bisherigen Überlegungen wurde als Grundlage für die Massenabschätzung eine Breite von $BCB=4,5m$ angenommen. Mit einer Schwimmerbreite von $B_{hull} \simeq 2,0m$ ergibt das eine ungefähre Breite über alles $BOA=2*BCB+B_{hull} \simeq 11,0m$.
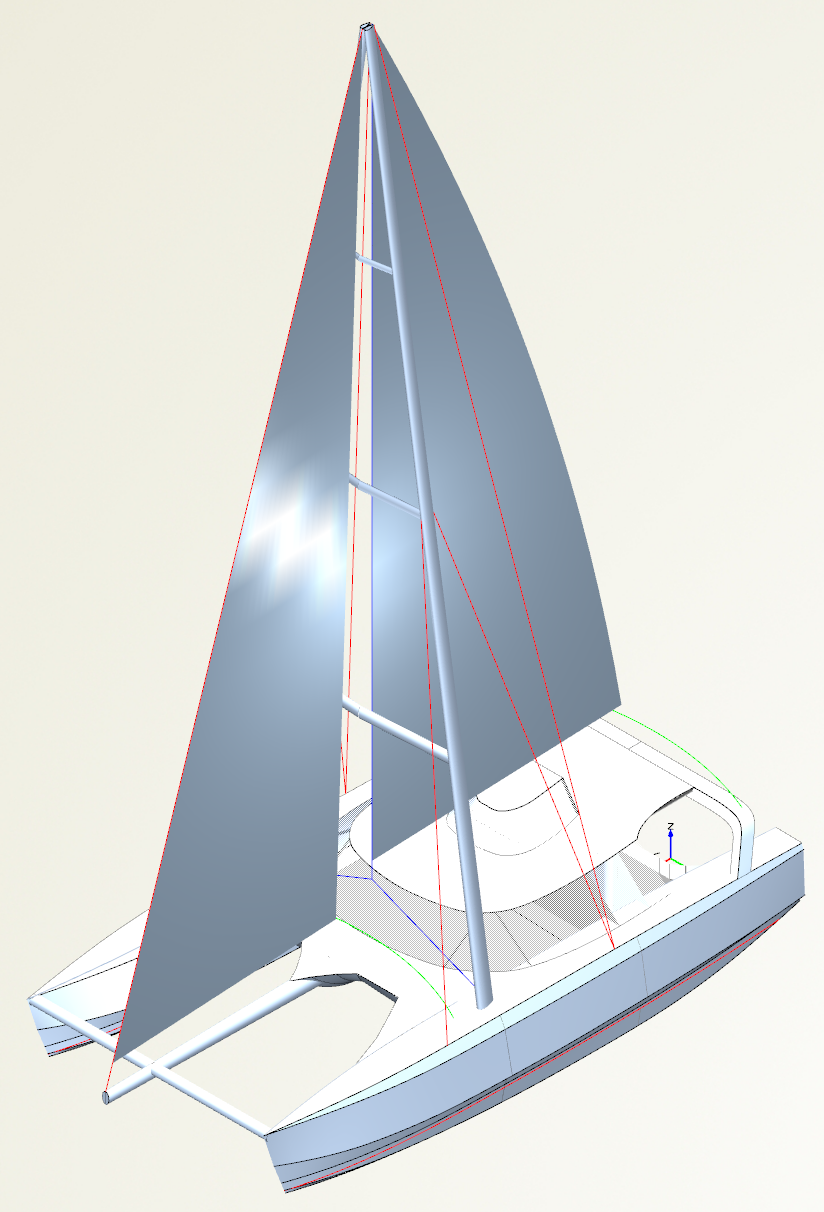
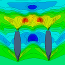
Abbildung 4: Modell 0 mit Segel (2013)
2013 habe ich das Modell etwas weiter verfeinert, um Flächen und somit Massen für eine genauere Massenabschätzung der Rumpfstruktur bestimmen zu können. Jetzt gibt es ein Steuerhaus, den Steuerstand und die Hauptspanten. Auch die Quer- und Längsträgermaße können bestimmt werden, und werden bei der Auslegung nach GL Richtlinien verwendet. Dort finden sich auch entsprechende Abbildungen.
Darüber hinaus enthält das Modell auch die Mast- und Segelstruktur, um eine grobe Übersicht über Mast- und Segelgeometrie zu bekommen (incl. Segelflächenabschätzung).
Da ich mich immer wieder auf dieses Modell beziehe, können die Bilder als Gedankenstütze dienen.
Parametrisches Modell
Die ganze Zeit ist von parametrischen
Schwimmern und Parametrisierung die Rede.
Doch was ist das? Und warum ist es nützlich? Bei einem Entwurf möchte man
möglichst viele sinnvolle Designvarianten ausprobieren oder noch besser
im
Hinblick auf eine Zielfunktion optimieren. Dazu muß aber der Rumpf
leicht, am besten automatisch, veränderbar sein und dabei auch keine
ungewollten Knicke oder Dellen bekommen. Die Alternative ist, für jeden
Einzelfall ein neues 3D-Modell zu machen. Da man das nicht in fünf Minuten
erledigt, ist das ein immenser Zeitaufwand. Eine automatische
Optimierung auf eine Zielfunktion ist damit gar nicht möglich. Das
schwierige bei parametrischen Modellen ist, die Zahl der Parameter so
gering wie möglich zu halten, ohne dabei im Vorfeld sinnvolle
Designvarianten auszuschließen. Am Ende wird das immer ein Kompromiss,
denn bei nur 6 Parametern und 10 möglichen Ausprägungen pro Parameter
reden wir schon über eine Million Varianten. Will man die zu
Übersichtszwecken alle auswerten, ist man sehr lange beschäftigt. Eine
Gesamtuntersuchung eines zu großen Suchraumes ist somit nicht sinnvoll.
Man muss also von einem
möglichst guten Entwurf ausgehen und dann per Zielfunktion festlegen,
wohin die Reise gehen soll, um das Design zu optimieren. Das erfolgt in
der Regel schrittweise: Zunächst kann man sich auf hydrostatische
Kennzahlen beschränken. Eine sinnvolle Aufgabe ist zum Beispiel, die
benetzte Fläche bei gegebener Verdrängung zu minimieren, wobei man
beispielsweise ein minimales Längen-/Breitenverhältnis als
zusätzliche Beschränkung berücksichtigt.
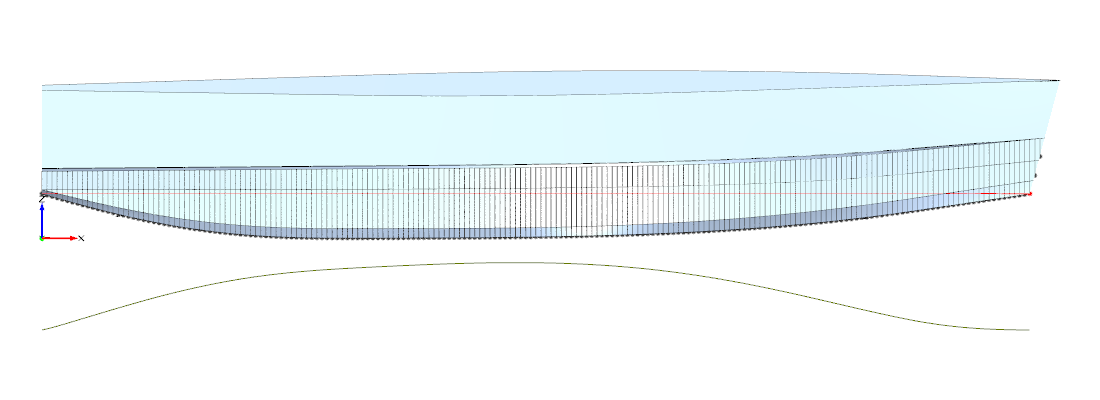
Abbildung 5: DreamcatcherOne-Entwurf 2011, Spantflächenkurve
Aber woher bekommt man ein gutes Ausgangsdesign? Da hilft nur
Fachliteratur weiter. Um es kurz zu machen: Auf Deutsch habe ich kein
vernünftiges Buch über Yachtdesign gefunden. Das beste Buch zum Thema
ist Principles of Yacht Design
von Lars Larsson und Rolf
E. Eliasson aus Schweden. Da stimmt jede Formel und alle Bezeichnungen
sind eindeutig. Zum Thema Katamarandesign
habe ich in Buchform
gar nichts gefunden. Allerdings gibt es eine sehr gute kurze Übersicht
von Terho Halme How
to dimension a sailing catamaran?
. Darüber hinaus hat auch John
Shuttleworth
in den 90er Jahren des vergangenen Jahrtausends einige
Zeitschriftenartikel geschrieben, die einen kleinen Eindruck
vermitteln, worauf es ankommt. Da die Datenbasis hier eher dürftig ist,
muss ich nach trail-and-error
-Verfahren vorgehen und die
Entwürfe, die ich für gut halte, mit Hilfe von
CFD-FEA (Computational Fluid Dynamics Finite Element Analysis)
analysieren.
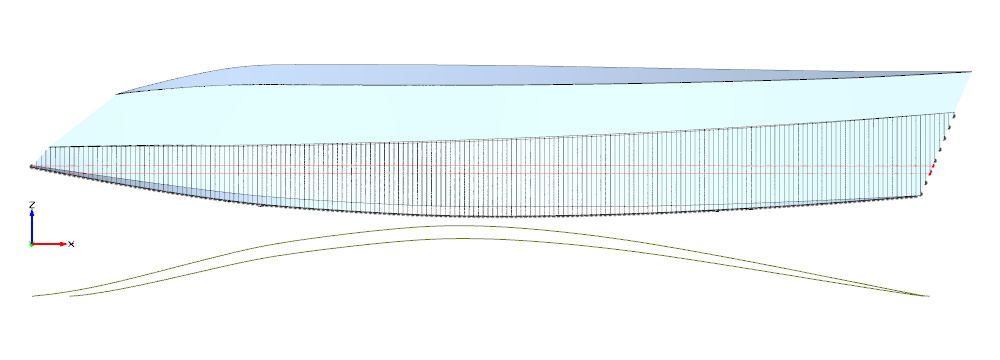
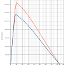
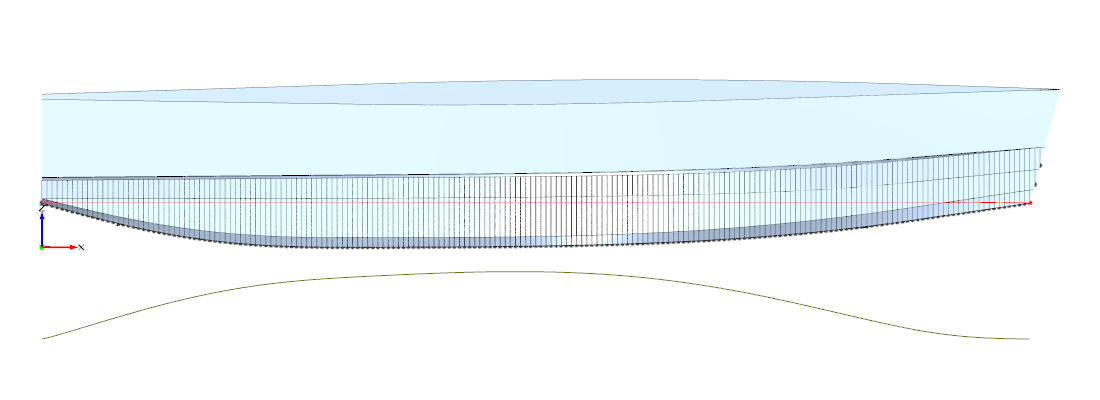
Abbildung 6: Vergleichskat, Spantflächenkurven und Wasserlinie
für 1,35m und 1,50m Tiefgang
Darüber hinaus ist es hilfreich, das eigene Design, mit bereits
gebauten Designs zu vergleichen. Dies ist wohl der klassischste Ansatz
überhaupt im Schiffsbau. Das Problem in meinem Fall ist, dass
ich sehr spezielle Anforderungen habe: Ich möchte aus Aluminium und in
Knickspantbauweise bauen. Da ist die Auswahl an vergleichbaren Designs
ziemlich gering. Immerhin
konnte ich bisher wenigstens ein solches Design auftreiben, das zudem
noch in den Dimensionen
vergleichbar ist: Aus den Plänen der Spanten habe ich in Friendship ein
3D-Modell rekonstruiert und die wichtigsten hydrostatischen Kennzahlen
meines ersten parametrischen Entwurfs (DCOne) dem Vergleichsdesign
(Kat) gegenübergestellt. Der Vergleichskatamaran ist zweimal
angegeben: Einmal wie er heute tatsächlich fährt (mit 1,50m Tiefgang)
und einmal, wie er im
Design (mit 1,35m Tiefgang) geplant war. Der Unterschied liegt in etwa
6 Tonnen Übergewicht, das auf Grund einer schwerer als geplanten
Aluminiumkonstruktion zustande kam.
Betrachtet wird in allen Fällen nur der Canoe-Body
also ohne
Anhänge. Die Tabelle zeigt, wie extrem wichtig eine genaue und
immer wieder verfeinerte Massenberechnung ist, der im Zweifelsfall ein
Re-design folgen muss. Im Design war der
Vergleichskat durchaus mit dem DCOne-Design vergleichbar, wenn
auch mit kleinen Abstrichen: So ist die benetzte Fläche
unverhältnismäßg groß
und auch die Lage von XCB und XCF zueinander lassen erwarten, dass der
Kat zum Nicken neigt. Genau dieses Verhalten konnte ich beim Mitsegeln
auf diesem Katamaran in der Praxis bestätigen. Dass die benetzte Fläche
des
Vergleichskats groß ist und somit die Leichtwindperformance
beeinträchtigt ist, kann man auch an dem Koeffizienten der größten
Spantfläche Cm ablesen: Dieser setzt die größte Spantfläche AX ins Verhältnis
mit BWL×Draft.
Ein optimaler, weil flächenminimaler, Wert läge bei π / 4, also rund
bei 0,785. Während sich das DCOne-Design mit 0,818, diesem Wert
annähert, liegt der Vergleichskat bei 0,511 bzw. 0,418 weitab vom
Optimum. Ein weiterer Performancekiller des Vergleichskats ist der neue
Tiefgang: Während im Design der Heckspiegel weit über der Wasserline
lag, taucht dieser nun ca. 1,5 cm ein. Dies begünstigt ein Festsaugen
des Hecks, da der Heckspiegel dafür nicht konzipiert war.
Jeder Jollensegler hat diesen Effekt schon einmal erlebt.
| Parameter | DCOne | Vergleichs-Kat real (1.5m Tiefgang) | Vergleichs-Kat Design (1.35m Tiefgang) |
|---|---|---|---|
| AW Wasserlinienfläche [m²] | 26,312 | 20,777 | 19,294 |
| AX Größte Spantfläche [m²] | 1,322 | 1,352 | 1,105 |
| BWL Größte Breite der Wasserlinie [m] | 1,842 | 2,153 | 1,602 |
| Cb Blockkoeffizient | 0,51 | 0,247 | 0,301 |
| Cm Koeffzient der größten Spantfläche | 0,818 | 0,418 | 0,511 |
| Cp Prismatischer Koeffizient | 0,624 | 0,591 | 0,589 |
| Cw Wasserlinienflächenkoeffizient | 0,736 | 0,564 | 0,735 |
| DISPM Verdrängte Masse (Salzwasser) [t] | 16,402 | 14,01 | 10,921 |
| DISPVOL Verdrängtes Volumen [m³] | 16,002 | 13,669 | 10,655 |
| Draft Tiefgang [m] | 0,87 | 0,957 | 0,807 |
| KML Metazentrische Höhe in Längsrichtung [m] | 35,773 | 24,559 | 27,391 |
| LB Längen/Breitenverhältnis | 10,531 | 7,941 | 10,223 |
| LOA Länge über alles [m] |
20,0 |
18,0 |
18,0 |
| LWL Länge der Wasserlinie [m] | 19,4 | 17,1 | 16,38 |
| S Benetzte Fläche [m²] | 43,021 | 39,059 | 33,331 |
| Tpc Verdrängungszunahme bei 1cm Tiefertauchung [m³] | 0,264 | 0,209 | 0,194 |
| XCB Auftriebsschwerpunkt in Längsrichtung vom Heck [m] | 8,793 | 8,518 | 8,698 |
| XCBp XCB auf LOA (Länge ü. Alles) bezogen [%] | 43,966 | 47,326 | 48,322 |
| XCF Schwerpunkt von AX vom Heck [m] | 8,948 | 7,793 | 8,024 |
| XCFp XCF auf LOA bezogen [%] | 44,738 | 43,293 | 44,575 |
Es bleiben aber noch Fragen offen:
Es fällt auf, dass das Heck des DCOne-Entwurfs wesentlich steiler
ausläuft als bei dem Vergleichskat. Das könnte unter Umständen ein
Problem für das (Halb-)Gleiten des Designs werden. Als Faustregel gilt,
dass das Heck nicht steiler als mit 15° nach oben laufen darf, wenn
Gleiten möglich sein soll. Dieser Grenzwert wird zwar von dem Design
nicht erreicht oder überschritten, aber es ist sicher ein Punkt, den
man im Auge behalten sollte. Andererseits ist es auch nicht leicht
möglich, das Heck flacher zu gestalten: Nimmt man dort Volumen weg,
wandert XCB nach vorne, XCF hingegen bleibt, wo er ist. Als
Gegenmaßnahme kann man nur den Bug in der Wasserlinienebene bauchiger
machen. Macht man die Wasserlinienfläche am Heck schmaler, verliert man
dort auch Auftrieb. XCB würde genauso wie XCF tendenziell weiter nach
vorne wandern. Eine weitere Möglichkeit wäre es, auch Auftrieb im
Bugbereich zu reduzieren, was aber insgesamt zu einem weiter erhöhten
Auftriebsverlust führen würde... Einen Königsweg gibt es also nicht.
Antworten können hier nur noch detaillierte CFD-Analysen geben.