29.02.2016
Segelfläche und Flächenschwerpunkt des Vorsegels
Nachdem wir uns schon mit dem Großsegel etwas warmgelaufen haben, können wir dieselbe Hürde für das Vorsegel angehen. Die einschlägige Formel für die Vorsegelfläche nach ORC VPP Dokumentation lautet:
$\quad \begin{split} \text{(1)} \quad A_{Vor} = 0,1125JL(1,445 LPG & + 2 JGL + 2 JGM \\ & + 1,5 JGU + JGT + 0,5 JH)\end{split} $
Zum Vergleich nochmal die Großsegelformel:
$\quad \text{(2)} \quad A_{Groß} = {\frac {P}{8}} (E + 2 MGL + 2 MGM + 1,5 MGU + MGT + 0,5 HB)$
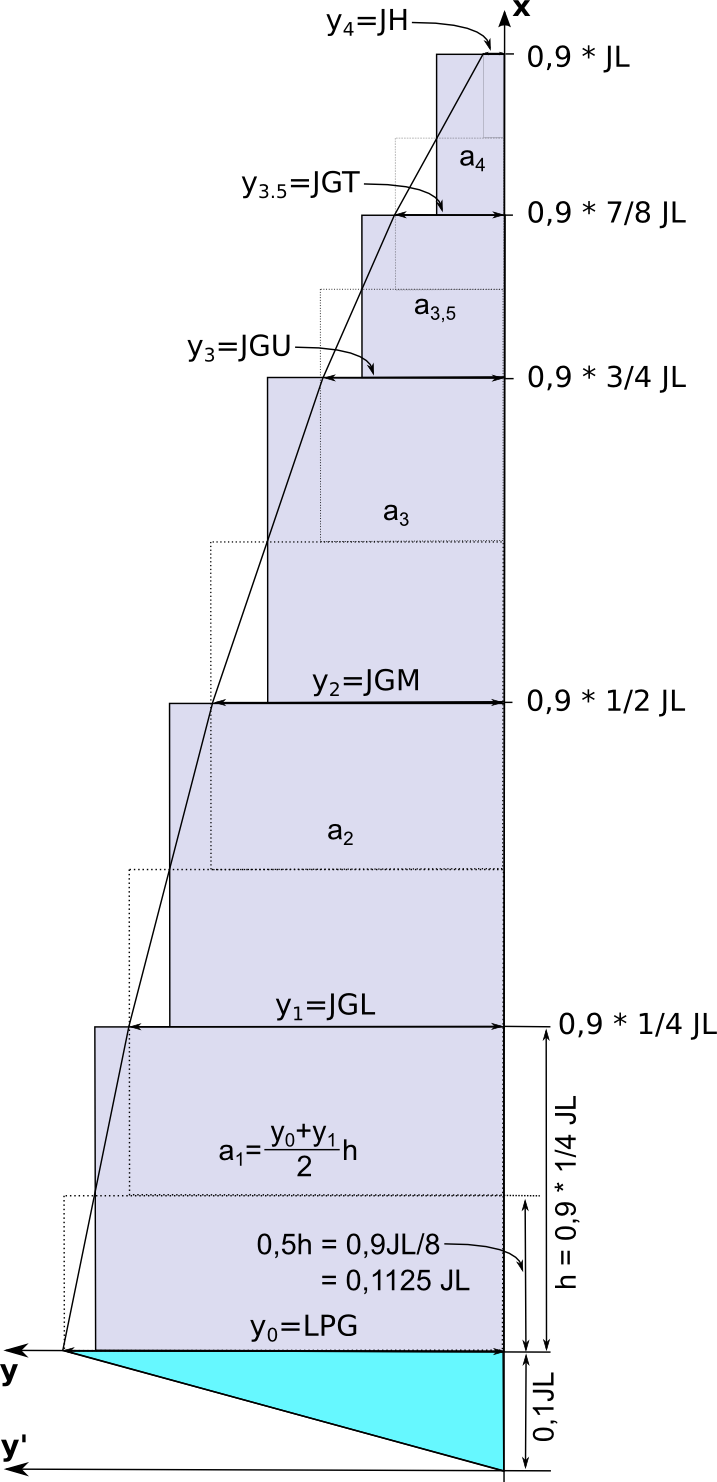
Abb. 1: Vorsegelmaße
Die Größen sind wie sie in Abbildung 1 definiert und haben in Analogie zum Großsegel die folgende Bedeutung:
| Bezeichner | Bedeutung | |
|---|---|---|
| 2015 | 2016 | |
| JL | HLU | Vorlieklänge (headsail luff length) |
| LPG | HLP | Größte Breite rechtwinkelig zum Vorliek (longest perpendicular girth/headsail luff perpendicular) |
| JGL | HQW | Vorsegelbreite unten (jib girth lower/headsail quarter width) |
| JGM | HHW | Vorsegelbreite mitte (jib girth middle/headsail half width) |
| JGU | HTW | Vorsegelbreite oben (jib girth upper/headsail threequarter width) |
| JGT | HUW | Vorsegelbreite top (jib girth top/headsail upper width (7/8th width)) |
| JH | HHB | Vorsegelkopfbrettbreite (headsail head board) |
Numerische Flächenberechnung ganz ohne Trapezregel
OK, die Zwischenüberschrift ist etwas gelogen, weil die Trapezregel natürlich schon in der Formel steckt, aber auf die erneute Herleitung wird hier verzichtet, weil die Flächenberechnung für das Großsegel mit Hilfe der Trapezregel recht geradlinig war. Das kann man für die Fock nicht mehr behaupten, weil in der Formel mehrere zusätzlich Annahmen und Ideen stecken, für die ich allerdings keine Dokumentation finden konnte. Daher war meine eigene Phantasie gefragt aus dem Vergleich mit der Großsegelformel, die ja sehr ähnlich, aber eben nicht gleich aussieht und den geometrischen Gegebenheiten des Vorsegels meine Schlüsse zu ziehen. Zu diesem Zweck habe ich in Abbildung 1 das Vorsegel so gedreht, dass auch hier wie beim Groß das Vorliek auf die $x$-Achse zu liegen kommt. Es fällt sofort auf, dass die Fock unten nicht parallel zur $y'$-Achse läuft. Weiterhin liegt LPG natürlich parallel zur $y$-Achse, da LPG definitionsgemäß senkrecht auf dem Vorliek stehen soll.
Abbildung 1 hilft auch, die Modifikationen der Vorsegelformel gegenüber der Großsegelformel
zu verstehen. In der Großsegelformel ist der Vorfaktor ${\frac{1}{8}}=0,125$ bei der
Vorsegelformel nur $0,1125$, also gerade 90% davon. Das bedeutet aber, dass die
numerische Integration der Fläche nur über $0,9JL$ erfolgt. In Abbildung 1 ist das so
dargestellt, dass die $y$-Achse um $0,1JL$ nach oben verschoben ist. Das Hauptintervall
$h$ für die numerische Integration ist also nicht ${\frac{1}{4}}JL$, sondern
$0,9 \cdot {\frac{1}{4}}JL$. Dem aufmerksamen Leser wird sofort ins Auge fallen,
dass bei dieser Integration das türkis-blaue Dreieck unten unterschlagen wurde.
Weiterhin fällt beim Vergleich von der Formeln (1) und (2) auf, dass die Faktoren vor
dem ersten Summenden (E bzw. LPG) verschieden sind. Die Vermutung liegt also nahe,
dass man die fehlende Dreiecksfläche durch diesen Faktor dazugemogelt hat. Ja,
dazugemogelt
ist wohl das richtige Wort, denn eine direkte mathematische
Ableitung ist mir dazu nicht eingefallen. Eine logische hingegen schon: Betrachten
wir das unterste gestrichelte Rechteck in Abbildung 1 so hat dieses die Maße
$\quad \text{(3)} \quad LPG \cdot 0,5h = LPG \cdot {\frac{0,9JL}{8}} = LPG \cdot 0,1125 JL$
Das türkis-blaue Dreieck hat die Maße $LPG \cdot 0,1 JL$, denn $0,1 JL$ ist gerade die vorher nicht berücksichtigte Restlänge des Vorlieks. Die Idee ist nun, die Fläche des türkis-blauen Dreiecks flächengleich als Aufschlag auf die Höhe LPG des ersten Rechtecks zu bestimmen. Annahme: Wäre die Sockelbreite des Dreiecks auf der $x$-Achse genauso breit wie die Sockelbreite des ersten Rechtecks, müsste man 0,5 LPG zu der Höhe LPG addieren (halbes Rechteck mit gleichen Maßen). Man würde also auf eine Höhe von 1,5 LPG kommen. Da jedoch die Sockelbreite des Dreiecks um den Faktor ${\frac{0,1JL}{0,1125JL}}$ kleiner ist als die des Rechtecks, muss auch die Fläche, aber auch der Höhenzuschlag auf LPG um diesen Faktor kleiner sein, also beträgt der Aufschlag ${0,5 \cdot \frac{0,1JL}{0,1125JL}} = 0,\overline{444}$. Somit müsste der erste Summand in Formel (1) $1,\overline{444}LPG$ lauten. Etwas kreativ auf die 3. Halbstelle gerundet ergibt das die 1,445 aus Formel (1).
Wie gesagt, diese Erklärung ist nur von mir erraten
. Aber nicht schlecht und
vor allem schlüssig würde ich sagen.
Numerische Berechnung des Flächenschwerpunkts mit der Trapezregel
Hier werde ich nur den schiffbaulichen Ansatz vorstellen. Da in diesem Fall die unterste Fläche unberücksichtigt bleibt, ergibt sich der Flächenschwerpunkt analog zu Formel (10) des Großsegels zu:
$\quad \text{(4)} \quad M_{yy}^S = {\frac {JL^2}{4^2\cdot 4}} (4 JGL + 8 JGM + 9 JGU + 7 JGT + 4 JH)$

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998