05.05.2015
SHIPFLOW Finale Ergebnisse
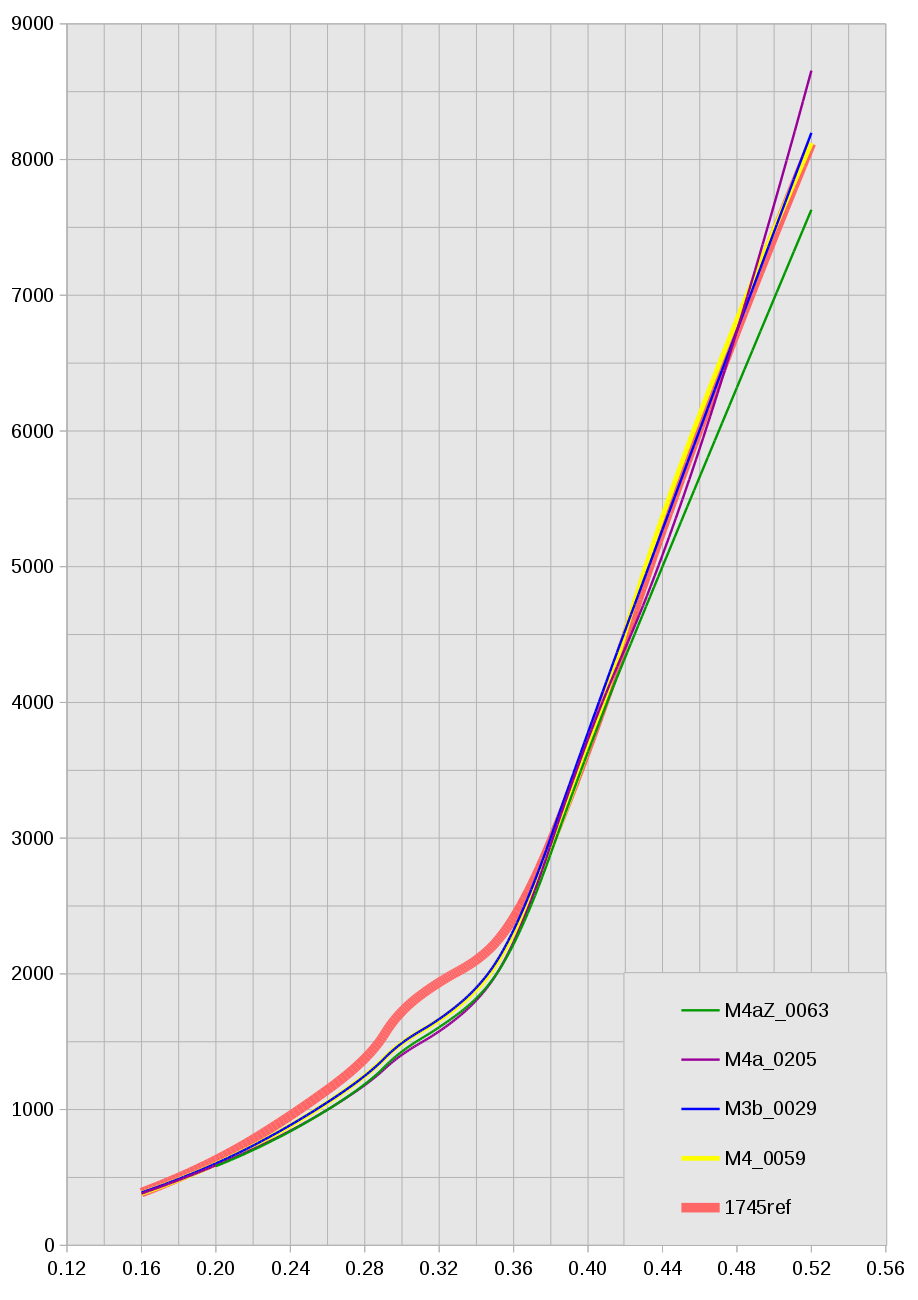
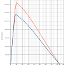
Abb. 1: Gesamtwiderstandskurven

Abb. 1: Gesamtwiderstandskurven
Insgesamt habe ich 6330 Parameterkombinationen untersucht.
Davon führten 4508 Kombinationen zu validen Rumpfformen, die alle Randbedingungen
(z.B. Verdrängung) erfüllen konnten und einer CFD-Analyse unterzogen wurden.
Davon wiederum habe ich 3987 Modell nur hinsichtlich ihres Wellenwiderstands untersucht
und die restlichen 521 zusätzlich auch in Hinblick auf den Gesamtwiderstand.
Alle Modelle wurden im Maßstab 1:1 berechnet. In wie weit das bei dem
zonal
-Ansatz tatsächlich von Bedeutung ist, vermag ich nicht zu sagen.
Zumindest bei dem
RANSE-Teil ist zumidest ein Einfluss wegen sonst fehlender Reynolds-Ähnlichkeit
möglich (vgl. Hochkirch 2013).
Bei der Auswahl der geeignetsten Einzelrumpfformen bin ich in mehreren
Schritten vorgegangen.
Im Schritt 1 habe ich für 2082 Designs die Wellenwiderstände für meine
Ausgangsmodellreihe Modell 3
(M3) berechnet.
Dabei sind einige kleinere Modellfehler und ungeeignete Parameterbereiche
zu Tage getreten, so dass ein Modell 3a und schließlich 3b erforderlich waren, wobei
ich vom Modell 3b für weitere 1472 Modelle den Wellenwiderstand berechnet habe.
Bei Modell 4 folgten weitere 432 Modelle.
Schritt 2: Mit dem besten Parameterbereich habe ich dann zwischen 150 und 200 Designs
für jedes der Modelle M3b, M4 und M4a im
zonal
-Verfahren mit SHIPFLOW gerechnet, um die Gesamtwiderstandswerte
der besten Designs vergleichen zu können.
Jedes dieser Modelle benötigt etwa 4-6 Stunden pro Geschwindigkeit (Froudezahl).
Dabei wurden nur die Froudezahlen $F_{n}=0,3$ und $F_{n}=0,44$ berechnet. Wer gut
im Kopfrechnen ist, wird bemerken, dass ich meine zwei Rechner damit monatelang
beschäftigt habe.
Schließlich habe ich in Schritt 3 für die ausgewählten eine Widerstandskurve für
$F_{n}=0.16/0.2 ... 0.52/0.64$ berechnet, um die Unterschiede sichtbar zu machen.
Auf Grundlage dieser Berechnungen habe ich anhand der
Wellen- und Gesamtwiderstände die besten Modelle M3b_0028, M4_0059, M4a_0063
und M4a_0206 aus den Modellreihen M3b, M4 und M4a ausgewählt. Eine detaillierter
Vergleich der Rumpfgeometrien der ausgewählten Modelle findet sich
hier). Die
mathematischen Grundlagen der Modellreihen finden sich unter dem Menüpunkt Modelle
.
Die beiden Werte der Froudezahl $F_{n}=0,3$ und $F_{n}=0,44$ habe ich gewählt, weil sie den gesamten Bereich, der für mich von Interesse ist ($F_{n}=0,15$ (ca. 4 Knoten) bis $F_{n}=0,52$ (ca.14 Knoten)), sehr gut repräsentieren. Bei $F_{n}=0,3$ tritt der erste größere Wellenwiderstandsberg auf, den es zu minimieren gilt. $F_{n}=0,44$ ist ein guter Repräsentant für den Widerstand bei etwas mehr als Rumpfgeschwindigkeit. Er lässt erahnen, wie steil der Widerstandsberg zum (Halb-)Gleiten hin ausfällt.
Abbildung 1 zeigt die Gesamtwiderstandskurven eines Rumpfes im Bereich $F_{n} = 0.16$
bis $F_{n} = 0.52$. Deutlich zu erkennten ist, dass das händisch konstruierte Modell
1745ref eine deutliche Widerstandserhöhung im Bereich $F_{n} = 0.30$
bis $F_{n} = 0.34$ aufweist. Alle computer-optimierten Modelle weisen diesen
Berg
nicht auf. Dafür unterscheiden sie sich am oberen Ende der Skala wider
recht deutlich. Auf Grund dieser Kurven halte ich das Modell M4aZ_0063 (hier immer
verkürzt so für M4aZnb_0063 aus dem Modellvergleich)
für das beste Modell, das ich gefunden habe. Darüber hinaus weist M4aZ_0063 noch weitere
günstige Eigenschaften auf:
- Der reine Rumpftiefgang ist minimal mit nur 97 cm.
- L/B liegt bei fast 11, was für einen schweren Fahrtenkatamaran ein sehr guter Wert ist.
- $C_{p}=0.595$ liegt am oberen Ende meiner gewünschten $C_p$-Skala, was die bessere Performance bei größeren Froudezahlen erklärt.
- XCB und XCF liegen dicht beieinander (Abstand nur 1,42% LWL).
- Am Heck weisen die Plattenenden eine relativ einheitliche Breite auf, was sich besser fertigen lässt.
Einziger Wermutstropfen, den alle M4Z-Modelle teilen ist die starke Plattenverschränkung im Bugbereich. Was fertigungs-technisch eine Herausforderung darstellt, hat aber segel-technisch auch Vorteile: Die stärkere Krümmung nach außen sorgt für ein trockeneres Deck auf See.
| 1745 _ref | M3bZ _0028 | M4Z _0059 | M4aZnb _0063 | M4aZnb _0205 | |
|---|---|---|---|---|---|
| $R_{t} (F_{n}=0,3)$ | 1723 | 1490 | 1489 | 1428 | 1403 |
| $R_{w} (F_{n}=0,3)$ | 676 | 458 | 471 | 429 | 381 |
| $R_{t} (F_{n}=0,44)$ | 5277 | 5274 | 5369 | 5195 | 5371 |
| $R_{w} (F_{n}=0,44)$ | 2682 | 2929 | 2939 | 2863 | 2941 |
| Trimwinkel $(F_{n}=0,44)$ | 0,82 | 0,83 | 0,9 | 0,86 | 0,88 |
| BWL [m] | 1,6 | 1,9 | 1,82 | 1,84 | 1,86 |
| LWL [m] | 20,1 | 20,1 | 20,1 | 20,17 | 20,17 |
| LB | 12,6 | 10,6 | 11,02 | 10,95 | 10,84 |
| Tiefgang [m] | 1,05 | 1,015 | 0,99 | 0,97 | 0,98 |
| BTR | 1,52 | 1,87 | 1,85 | 1,9 | 1,9 |
| DISP [t] | 18,000 | 18,000 | 18,000 | 18,000 | 18,000 |
| BWL Heck [m] | 1,2 | 1,1 | 1 | 0,88 | 0,95 |
| Tiefgang Heck [m] | 0,05 | 0,075 | 0,075 | 0,075 | 0,075 |
| SecA | 1,38 | 1,49 | 1,48 | 1,46 | 1,5 |
| Benetzte Fläche [m²] | 46,7 | 46,1 | 46,1 | 46,4 | 46,5 |
| WPA [m²] | 26,9 | 29,6 | 28,6 | 28,9 | 29,3 |
| Tpc [kg] | 277 | 303 | 293 | 296 | 298 |
| Cp | 0,634 | 0,588 | 0,591 | 0,595 | 0,582 |
| Cb | 0,52 | 0,45 | 0,49 | 0,49 | 0,48 |
| Cm | 0,82 | 0,77 | 0,82 | 0,82 | 0,82 |
| Cw | 0,838 | 0,77 | 0,78 | 0,78 | 0,77 |
| XCB_st0 | 51,77 | 51,57 | 52,42 | 52,06 | 52,48 |
| XCF_st0 | 53,95 | 54,04 | 53,91 | 53,48 | 54,33 |
| XCB vom Heck [m] | 9,69 | 9,73 | 9,56 | 9,67 | 9,59 |
| XCF vom Heck [m] | 9,25 | 9,24 | 9,26 | 9,39 | 9,21 |
Alle Widerstandswerte wurden mit $g = {9.80665 {{kg*m} \over {s^2}}}$, kinematische Viskosität des Salzwassers bei 20°C ${\eta = 1.0508*10^{-6}} {{m^2} \over {s}}$ und der Salzwasserdichte bei 20 Grad $\rho = 1024.8103 {kg \over {m^3}}$ berechnet. Daraus wurde jeweils die Reynoldszahl für für die reale Schiffslänge (nicht skaliert) für die verschiedenen Froudezahlen ermittelt. Sie liegen im Bereich $R_{n (Fn=0.16)} = 4.2966621 * 10^7$ bis $R_{n (Fn=0.64)}=1.7186648 * 10^8$.
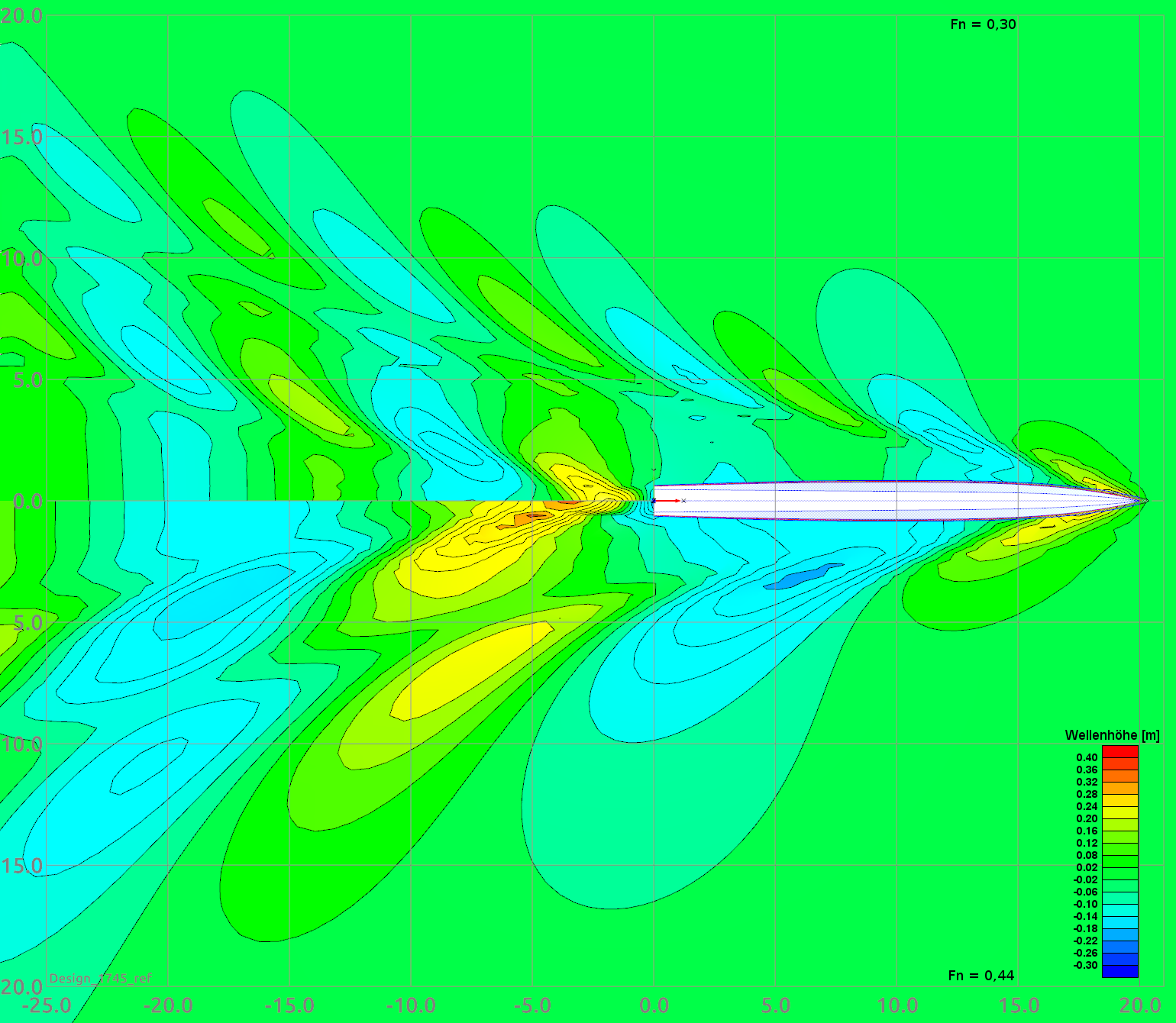
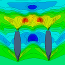
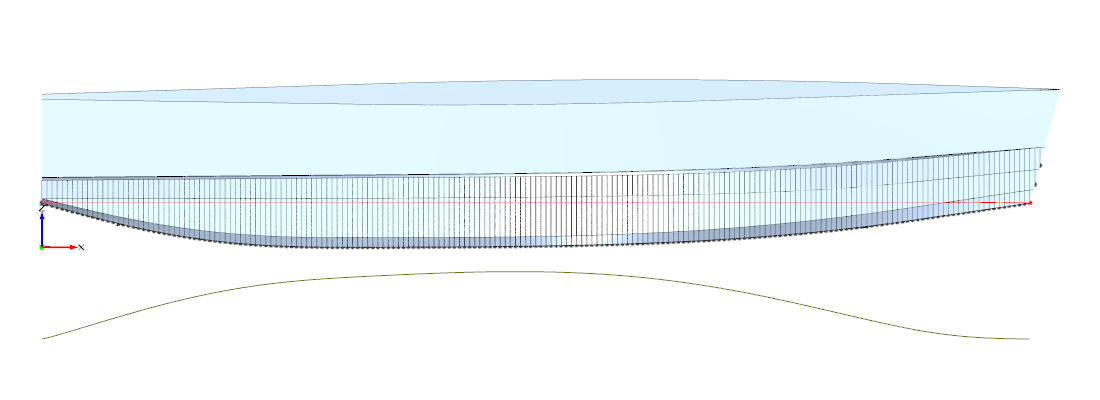
Abb. 2: Referenzmodell Design 1745ref
Abbildungen 2-6 zeigen die Wellenbilder der Ausgewählten Designs jeweils für $F_{n}=0,3$ (obere Hälfte) und $F_{n}=0,44$ (untere Hälfte). Alle Bilder wurden farblich auf denselben Wellenhöhenbereich von -0.2m bis +0.4m bei gleicher Anzahl von Farben kalibriert, so dass eine direkte Vergleichbarkeit aller Darstellungen gegeben.
In der oberen Hälfte des Referenzmodells 1745ref kann man auch am Wellenbild erkennen, dass bei $F_{n}=0.3$ größer sein muss, als bei den anderen Modellen: Die Wellenhöhenverteilung entlang des Rumpfes ist deutlich unruhiger und zeigt auch höhere Amplituden.
Bei $F_{n}=0.44$ erkennt man gut, dass das Design M4aZ_0063 bei einem gleichförmigen Wellenbild geringere Amplituden als alle anderen Designs aufweist. Auch dies steht im Einklang mit den numerischen Werten.
Es bleibt abzuwarten, ob diese Ergebnisse zumindest qualitativ mit NUMECA Fine/Marine bestätigt werden können.
_waves_030_044_wh.png)
Abb. 3: Drei-Knickmodell M3bZ_0028
_waves_030_044_wh.png)
Abb. 4: Vier-Knickmodell M4Z_0059
_waves_030_044_wh.png)
Abb. 5: Vier-Knickmodell M4aZ_0063
_waves_030_044_wh.png)
Abb. 6: Vier-Knickmodell M4aZ_0205

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998