01.02.2016
Velocity Prediction Programm (VPP)
VPP hat sich für mich immer als etwas für Reagattafetischisten angehört. Das stimmt so nicht. Tatsache ist, dass man für jedes Segelbootdesign in der Designphase eine VPP-Berechnung machen sollte, damit das Design später auch die gewünschte Performanz erreicht.
Jeder redet über VPP und es wird sehr viel darüber geschrieben, aber am Ende des Tages geht das Wissen oft darüber über das Anschauen von Polardiagrammen nicht hinaus. Die kommerziellen VPP-Programme rangieren zwischen teuer und unverschämt. Das günstigste ist noch das Programm vom ORC, das zur Zeit (2015) für 500€ Jahresmiete zu haben ist. Leider hat es einen kleinen Fehler: Es behandelt nur Einrumpfboote. Das mag daran liegen, dass die Datenbasis der Delft Systematic Yacht Hull Series, auf der der hydrodynamische Teil dieses Programms beruht, nicht ausreichend Katamranmodelle zur Verfügung stellt oder aber auch daran, dass die VPP-Rechnung für Katamarane etwas anders funktioniert. Also werde ich mein eigenes Velocity Prediction Programm schreiben (müssen). Die Darstellungen zu diesem Thema sind oft recht unübersichtlich. Daher werde ich das Verfahren Top-Down darstellen: Von der groben Übersicht bis ins Unterholz der einzelnen Teilaspekte.
Was rechnet ein VPP?
Grundsätzlich tut ein VPP nichts anderes als auf Grundlage von Boots- und Segelgeometrie Gleichgewichtsgleichungen zwischen aerodynamischen Größen $\sqcup^A$ und hydrodynamischen Größen $\sqcup^H$ zu lösen. Diesem Ansatz liegt die durchaus sinnvolle Annahme zu Grunde, dass man aero- und hydrodynamische Größen getrennt betrachten kann. Welche Größen und wie viele es sind, hängt davon ab, wieviele unabhängige Variablen man bei der Rechnung berücksichtigt.
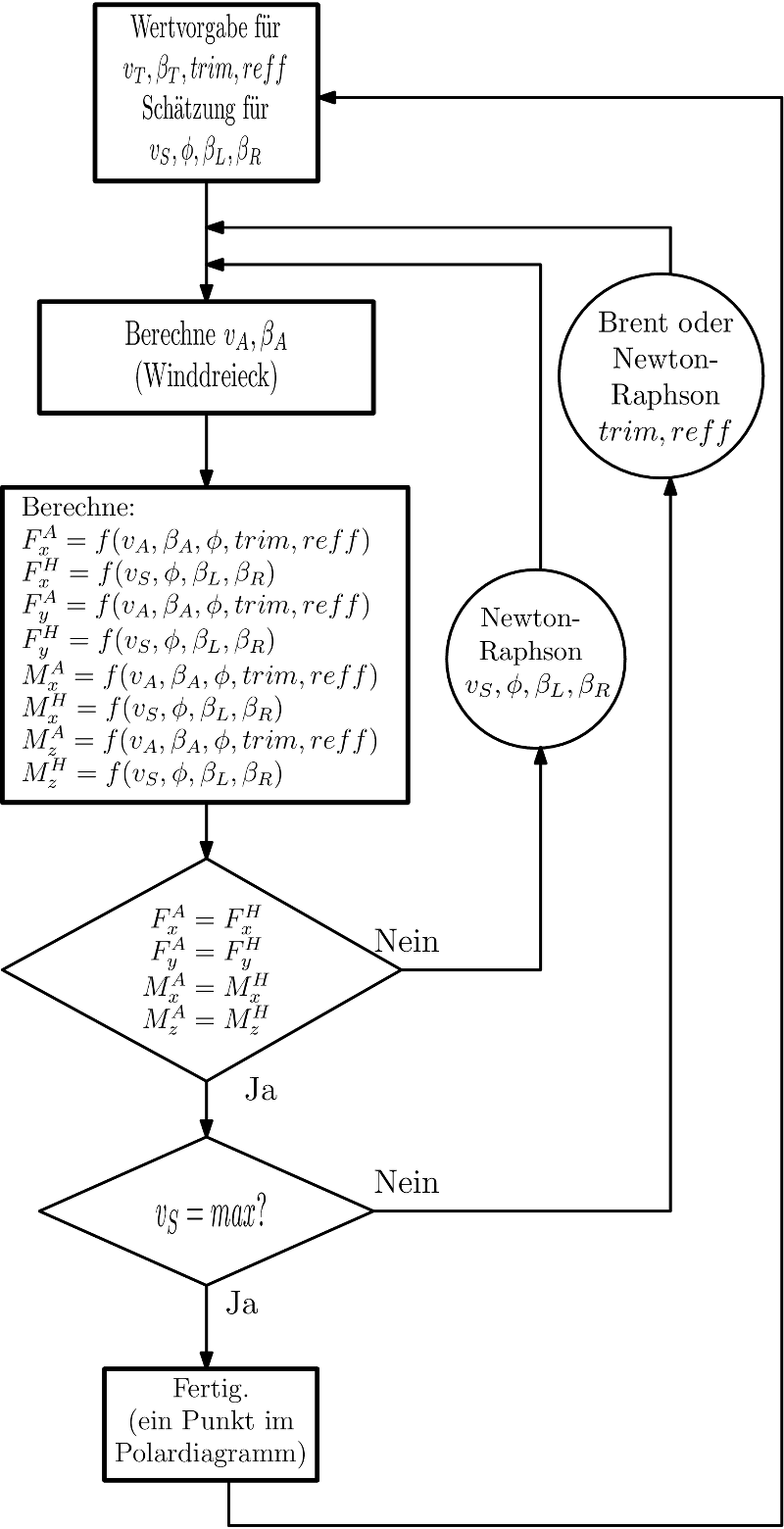
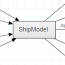
Abbildung 1: VPP - Funktionsprinzip
Zur leichteren Orientierung werde ich die Benennungen dieser Größen gemäß den Achsen des Schiffkoordinatensystems $x, y, z$ vornehmen. Das Koordinatensystem $x, y, z$ ist ein Rechtssystem, wobei die positive x-Achse in Fahrtrichtung des Schiffes zeigt, die y-Achse nach Backbord (in Fahrtrichtung links) und die z-Achse nach oben. Demnach weist es einen mathematisch positiven Drehsinn auf. Positive Winkel werden also entgegen dem Uhrzeigersinn aufgetragen.
Für einen vollständigen Parametersatz benötigt man sechs Gleichgewichtsgleichungen, drei Kräftegleichgewichte und drei Momentengleichgewichte.
Um die Gleichgewichtssituation eines gängigen Segelbootes aus seglerischer Sicht gut abbilden zu können, sollten vier Gleichungen aufgestellt werden, um die folgenden vier Variablen berechnen zu können:
| Schiffsgeschwindigkeit | $v_S$ |
| Krängungswinkel | $\phi$ |
Abdriftwinkel (Lwie leeway) | $\beta_L$ |
| Ruderwinkel | $\beta_R$ |
Die vier zugehörigen Gleichgewichtsgleichungen sind:
| Kräftegleichgewicht in Fahrtrichtung ($x$) | $F_x^A = F_x^H$ | $\text{(1)}$ |
| Kräftegleichgewicht quer zur Fahrtrichtung ($y$) | $F_y^A = F_y^H$ | $\text{(2)}$ |
| Momentengleichgewicht um die $x$-Achse (Krängung) | $M_x^A =M_x^H $ | $\text{(3)}$ |
| Momentengleichgewicht um die $z$-Achse (Gieren) | $M_z^A = M_z^H$ | $\text{(4)}$ |
Oft werden jedoch noch weiter vereinfachte Ansätze gewählt, wie zum Beispiel beim
ORC International
Verfahren (früher IMS). Laut deren Beschreibung benutzen sie
nur die Gleichungen (1) und (3). Dies hat zur Folge, dass das Verfahren keinen
Abdriftwinkel (leeway) und keine Ruderbalance bestimmen kann. Der Hintergrund ist, dass
der Lateraldruckpunkt der Segel in $x$-Richtung auf Grund der Verformungen der Segel
schwer mit einfachen Formeln zu bestimmen ist.
Man geht davon aus, dass die Yacht gut ausbalanciert
ist und mit kleinem Abdriftwinkel segelt, was auf moderne Designs durchaus zutrifft.
Das bedeutet aber auch, dass das Verfahren nach ORC unter Umständen
Segeltrim und -reffwerte annimmt, die so viel Druck auf dem Ruder erzeugen,
dass ein sinnvolles Steuern nicht möglich oder mit hohen Widerstandswerten durch extreme
Ruderausschläge und Abdriftwinkel verbunden ist. Interessanter finde ich,
dass dann auch der Abdriftwinkel $\beta_L$ als zu optimierende Größe wegfällt.
Da der induzierte Wasserwiderstand nicht unerheblich von dem Abdriftwinkel abhängt,
ist die Frage wie gut man das mit einem fixen Wert berücksichtigen kann. Es erscheint
daher sinnvoll, wenigstens den Abdriftwinkel mit Hilfe der Gleichung (2) einzubeziehen.
Das wird auch der Ansatz sein, den ich verfolgen werde.
Der Ablauf
Einen groben Überblick über den Ablauf einer VPP-Berechnung zeigt Abbildung 1. Das Verfahren zeigt drei Schleifen:
Die innerste findet mit Hilfe eines iterativen Newton-Raphson-Näherungsverfahrens den Gleichgewichtspunkt für eine fixe Kombination der Eingabeparametern $v_T, \beta_T, trim, reff$. Damit das Newtonverfahren schnell konvergiert, ist die anfängliche Schätzung für $v_S, \phi, \beta_A, \beta_R$ von entscheidender Bedeutung.
Was vielleicht nicht jedem geläufig ist, ist die Tatsache, dass jeder Kurvenpunkt, der auf einem Polardiagramm erscheint, das Resultat einer weiteren Optimierung ist. Die Eingabeparameter für diese Optimierung sind die Reff- und Trimmparameter der Segel. Diese Werte bestimmen ob die Segel flach oder bauchig getrimmt sind und wie groß die tatsächlich gesetzte Segelfläche ist. In der mittleren Schleife werden daher mit Hilfe eines weiteren Newton-Raphson- Näherungsverfahren oder auch eines Brent-Suchalgorithmus die Reff- und Trimparameter variiert bis die gefundene Bootsgeschwindigkeit $v_S$ maximal ist.
Dies ist auch der Punkt, an dem sich die Berechnung für Einrumpfboot und Katamarane fundamental unterscheidet: Bei Einrumpfbooten führt diese Suche zu einem stabilen Gleichgewicht: Hat man zu viel Segelfläche gesetzt oder sind die Segel zu bauchig, führt das zu starker Krängung des Schiffes, so dass der Wind nicht mehr so viel Angriffsfläche hat. Wie wir unten sehen werden, wird dieser Effekt als eine fiktive Reduktion der scheinbaren Windstärke berücksichtigt. Da der Hebelarm mit zunehmender Krängung wächst, stellt sich ein stabiles Gleichgewicht ein.
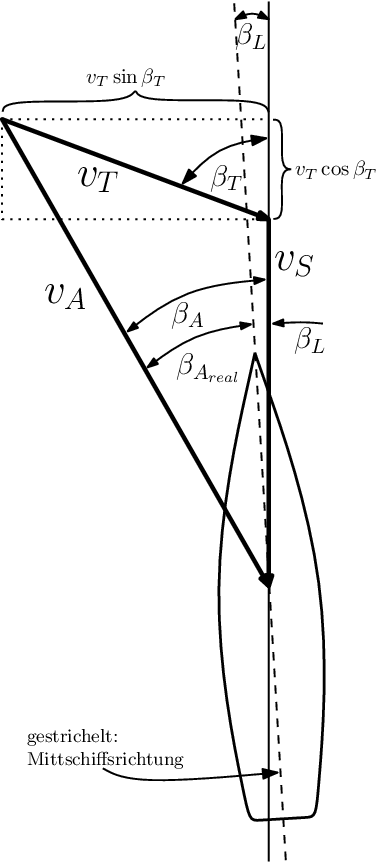
Abb. 2: Scheinbarer Wind
Beim Katamaran ist dies nicht der Fall: Da die Hebelarmkurve eines Katamarans bis zu Krängungswinkeln von etwa 10° steil ansteigt, das Schiff also sehr steif ist, würde die Einrumpfrechnung hier nicht zu einem stabilen Gleichgewicht führen: Die Geschwindigkeit würde bei geringen Krängungen immer weiter ansteigen, bis das Boot virtuell kentert. Deshalb muss man bei Katamaranen bei der Bestimmung von Trimm- und Reffparametern einen maximalen Krängungswinkel von 4-5° vorgeben. Da sich das Geschwindigkeitsmaximum bei höheren Windstärken immer bei diesem Maximalwinkel einstellen wird, spricht man auch davon, dass der Katamaran mit einem fixen aufrichtendem Moment fährt.
Das Ganze wird dann in der äußersten Schleife iterativ für die gewünschten wahren Windgeschwindigkeiten z.B. $v_T = 6, 8, 10, 12, 16, 20$ Knoten durchgeführt. Für jede Geschwindigkeit werden dann die gesuchten Einfallswinkel des wahren Windes z.B. $\beta_T = 35 ... 180°$ durchgerechnet. Im Ergebnis erhält man dann das bekannte Polardiagramm.
Scheinbarer Wind
Bevor die Berechnungen der innersten Schleife beginnen kann, müssen aus wahrem Wind $v_T$, dem Einfallswinkel des wahren Winds $\beta_T$ und der Schiffsgeschwindigkeit $v_S$ mit den Gleichungen (5) und (6) scheinbarer Wind $v_A$ und dessen Einfallswinkel $\beta_A$ berechnet werden, weil das aerodynamische Modell (Segelmodell) diese Werte benötigt.
$\quad \text{(5)} \qquad v_A = \sqrt{(v_T \cos \beta_T + v_S)^2 + (v_T \sin\beta_T)^2}$
$\quad \text{(6)} \qquad \beta_A = \arctan{ {v_T \sin \beta_T} \over {v_T \cos\beta_T + v_S}}$
Die zwei Gleichungen beschreiben die Projektion von $v_T$ auf $v_s$ zu der $v_S$ addiert wird und den Wert senkrecht dazu (Sinus-Term). Von diesem neuen Vektor wird der Betrag berechnet, so dass man $v_A$ erhält. Gleichung (6) ist dann lediglich der Richtungswinkel dieses neuen Vektors. Dabei wurde der Abdriftwinkel $\beta_L$ vernachlässigt, indem statt $\beta_{A_{real}} = \beta_A - \beta_L$ vereinfacht $\beta_{A_{real}} \approx \beta_A$ (Gleichung (6)) gesetzt wird, wie man in Abbildung 2 erkennen kann. Der Grund dafür ist naheliegend: Würde man $\beta_L$ hier einbeziehen, hätte man eine weitere Abhängigkeit geschaffen, die in der innersten Schleife durch eine weitere Gleichung ins Gleichgewicht gebracht werden müsste. Bezieht man $F_y^H$ in das Modell ein, ist das kein Problem und man könnte in jeder Iteration eine neues $v_A$ und $\beta_A$ bestimmen. Ist die Gleichgewichtsgleichung für $F_y^H$ nicht Teil des Modells, bleibt nur das Weglassen. Um Missverständnissen vorzubeugen: $v_T$ ist in Bezug auf die Bewegungsrichtung des Schiffs definiert (Richtung von $v_S$), die wegen der Abdrift nicht der Mittschiffsrichtung entspricht. $v_A$ hingegen ist gegenüber der Mittschiffslinie, also der gestrichelten Linie in Abbildung 2, definiert. $v_A$ repräsentiert nämlich, wie den meisten Seglern bekannt, den Wind, den die Segel und der Verklicker tatsächlich sehen. Verklicker und Segel sind aber an der Mittschiffslinie ausgerichtet. Man müsste also vorher $v_S$ auf die Mittschiffslinie projezieren ($v_{S_{mitt}} = v_S \cos \beta_L$). Da $\beta_L$ zumindest bei einem modernen Design mit Schwert oder schlankem Kiel maximal 4° betragen sollte, reden wir hier über einen Fehler von $1-\cos 4° \approx 0,2\%$.
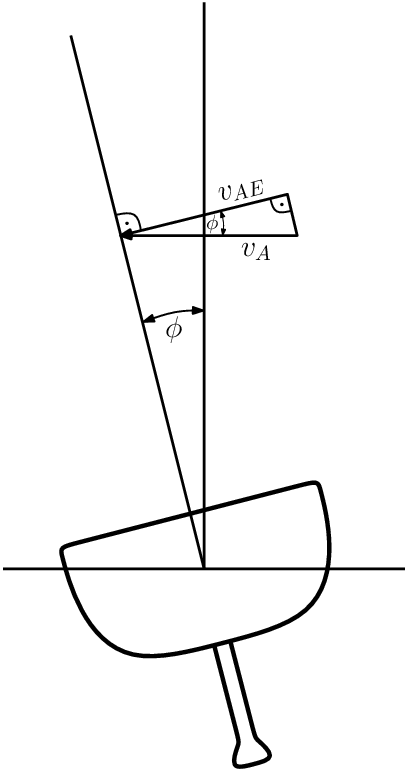
Abbildung 3: Effektiver Wind
Effektiver Wind
Der bisher gefundene scheinbare Wind gilt nur, wenn das Segelschiff aufrecht segelt. Da das physikalisch ausgeschlossen ist, kann man den Effekt der Krängung im Vorfeld berücksichtigen, indem man einen effektiven scheinbaren Wind $v_{AE}$ und den dazugehörigen effektiven Winkel des scheinbaren Windes $\beta_{AE}$ bestimmt, der den Krängungswinkel $\phi$ berücksichtigt. Diese Idee der Theorie des effektiven Einfallswinkels stammt von J.E. Kerwin (1978). Sie besagt, dass Vortrieb- und Widerstandskräfte der Segel von dem Wind abhängen, der in Fahrtrichtung gesehen rechtwinkelig zum Mast einfällt. Interessanterweise kommt diese Theorie den Messungen aus dem Windkanal recht nahe, weshalb man sie noch heutzutage benutzt. Die Formeln (5) und (6) werden unter Berücksichtigung des Krängungswinkels $\phi$ zu:
$\quad \text{(7)} \quad v_A = \sqrt{(v_T \cos \beta_T + v_S)^2 + (v_T \sin\beta_T \cos \phi)^2}$
$\quad \text{(8)} \quad \beta_A = \arctan{ {v_T \sin \beta_T \cos \phi} \over {v_T \cos\beta_T + v_S}}$
Da der Krängungswinkel $\phi$ sowieso durch das Momentengleichgewicht um die $x$-Achse bestimmt wird, kann man ihn in jeder Iteration berücksichtigen. Bei Einrumpfbooten ist das in Anbetracht von Krängungswinkeln von bis zu 30° unverzichtbar. Bei einem Katamaran mir einem maximalen Krängungswinkel von 5°, ist das entbehrlich, da die Abweichung maximal $0,4\%$ beträgt.
Windgeschwindigtkeitsänderung in Abhängikeit von der Höhe
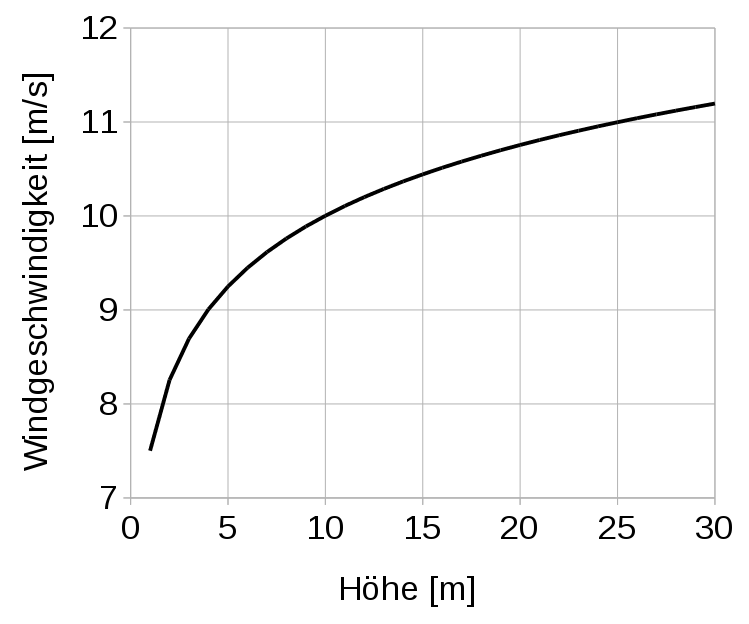
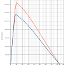
Abbildung 4: Beispiel $v_T(z)$
Will man den Effekt des Windes auf die Segel genau untersuchen, kommt man um die Verwendung eines Höhenprofils der Luftgrenzschicht über dem Wasser nicht vorbei. Die wahre Windgeschwindigkeit ist dann eine Funktion der Höhe $v_T = v_T(z)$. Neuere Segelmodelle für VPP berücksichtigen diese verschiedenen Windgeschwindigkeiten in verschiedenen Höhen in Form eines Faktors (twist).
Aber auch das Segelmodell nach Kerwin (kerwin1978) berücksichtigt den Gradienten dahingehend, dass die effektive Windgeschwindigkeit immer auf den Angriffspunkt (center of effort $CE_z$) des Riggs bezogen wird. Dieser aber hängt vom Krängungswinkel und dem Reffzustand des Riggs ab. Daher benötigt man eine Exponentialfunktion $v_T(z)$, die die Änderung der effektiven Windgeschwindigkeit in Abhängigkeit von der Höhe $z$ bestimmt. Umgerechnet in metrische Größen ergibt sich die Formel von Kerwin wie in (9) angegeben.
$\quad \text{(9)} \qquad v_T(z) = 0,1086 \cdot v_T(10m) \cdot ln(1000z)$
Der Faktor $0,1086$ ergibt sich daraus, dass Kurve durch den $v_T(10m)$, also den wahren Wind in 10 Metern Höhe gehen soll. Für $z=10m$ ist nämlich $0,1086 \cdot ln(1000\cdot10) = 1$. Abbildung 4 zeigt ein Beispiel für die Windstärkenänderung für $v_T(z=10m) = 10{m \over s}$
Hydrodynamisches und aerodynamisches Modell
Das physikalische Wissen über das Schiff steckt in dem hydrodynamischen und den aerodynamischen Modellen. Das hydrodynamische Modell beruht in der Regel auf Tanktests. In der Regel auf den Daten der verschiedenen Delft Systematic Series. Aus diesen Tanktest leitet man die Sensitivitäten der vier abhängigen Größen ${\partial{F_y^H}} \over {\partial{\beta}}$, ${\partial{F_x^H}} \over {\partial{(F_y^H)^2}}$, ${\partial{(M_x^H}-M_{xHS}^H)} \over {\partial{\beta}}$ und ${\partial{M_z^H}} \over {\partial{\beta}}$ für jede gemessene Kombination von Schiffsgeschwindigkeit $v_S$ und Krängungswinkel $\phi$ ab, um dadurch eine Linearisierung der Abhängigkeiten zu bekommen. In meinem konkreten Fall habe ich die Tanktests durch CFD-Simulationen ersetzt. Das Verfahren ist dasselbe. Da das verwendete aerodynamische Modell (Segelmodell) keinen Lateraldruckpunkt in $x$-Richtung liefert, bleibt bei mir auch im hydrodynamischen Modell $M_z^H$ außen vor.
Bei dem aerodynamischen Modell folge ich weitgehend
dem Segelmodell von Hazen (hazen1980) und dem
aktuellen Modell des Ratingssystems ORC International
(orc2015) - mit ein paar kleinen
Anpassungen für meinen Katamaran.

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998