01.05.2013
SHIPFLOW aus Sicht des Praktikers - Netzsensitivität (potential flow)
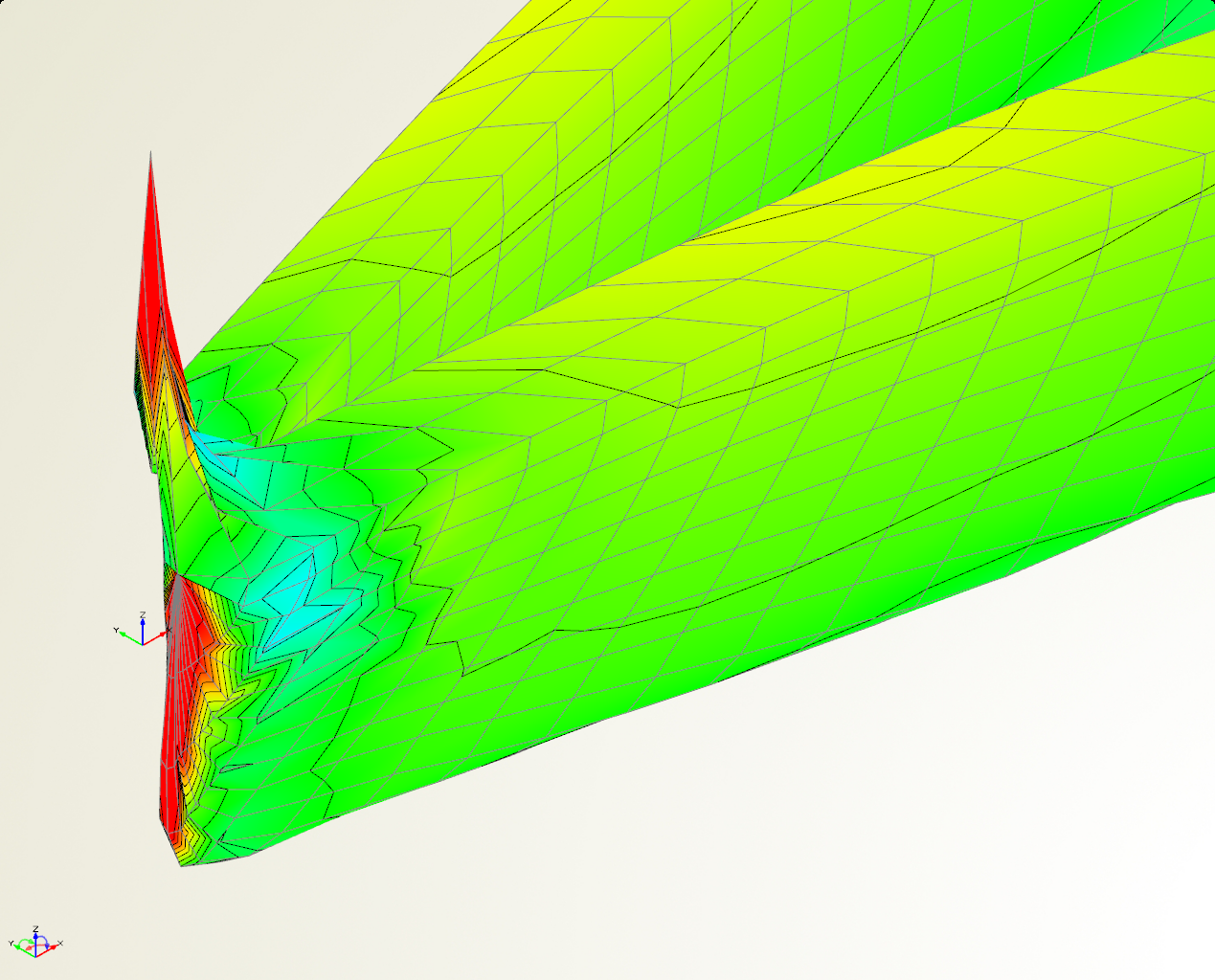
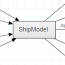
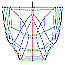
Abbildung 1: Netz am Bug (Buglinie, DENS 1,0)
Bei jeder verlässlichen CFD-Rechnung muss ausgeschlossen werden, dass die Berechnungsergebnisse von dem gewählten Netz abhängen. Darüber hinaus sollte das Netz die gewünschte Rumpfform möglichst gut nachbilden. Bei SHIPFLOW erfolgt die Vernetzung entweder vollautomatisch oder durch Vorgabe von Netzkennwerten wie Anzahl der Knoten und zusätzlich Ausdehnung in x-y-Richtung für die Wasseroberfläche.
Als zusätzliche Anforderung kam bei mir hinzu, dass das Netz für Froudezahlen zwischen $F_n$=0,2 und etwa 0,7 funktionieren muss. Es stellte sich bald heraus, dass die Netzausdehnung an die Froudezahl angepasst sein muss, damit die Berechung überhaupt konvergiert. Diese Größenanpassung erledigt SHIPFLOW sehr zuverlässig automatisch. Bei weiteren Versuchen zeigte sich, dass der Netzgenerator XMESH für XPAN auch ein halbautomatisches Verfahren beherrscht: Man kann die Netzauflösung für Rumpf und Wasserfläche als Netzauflösungskoeffizienten vorgeben und dennoch die automatische Netzgrößengenerierung von SHIPFLOW verwenden. Dies stellte sich als der praktikabelste Weg für die Netzuntersuchungen heraus.
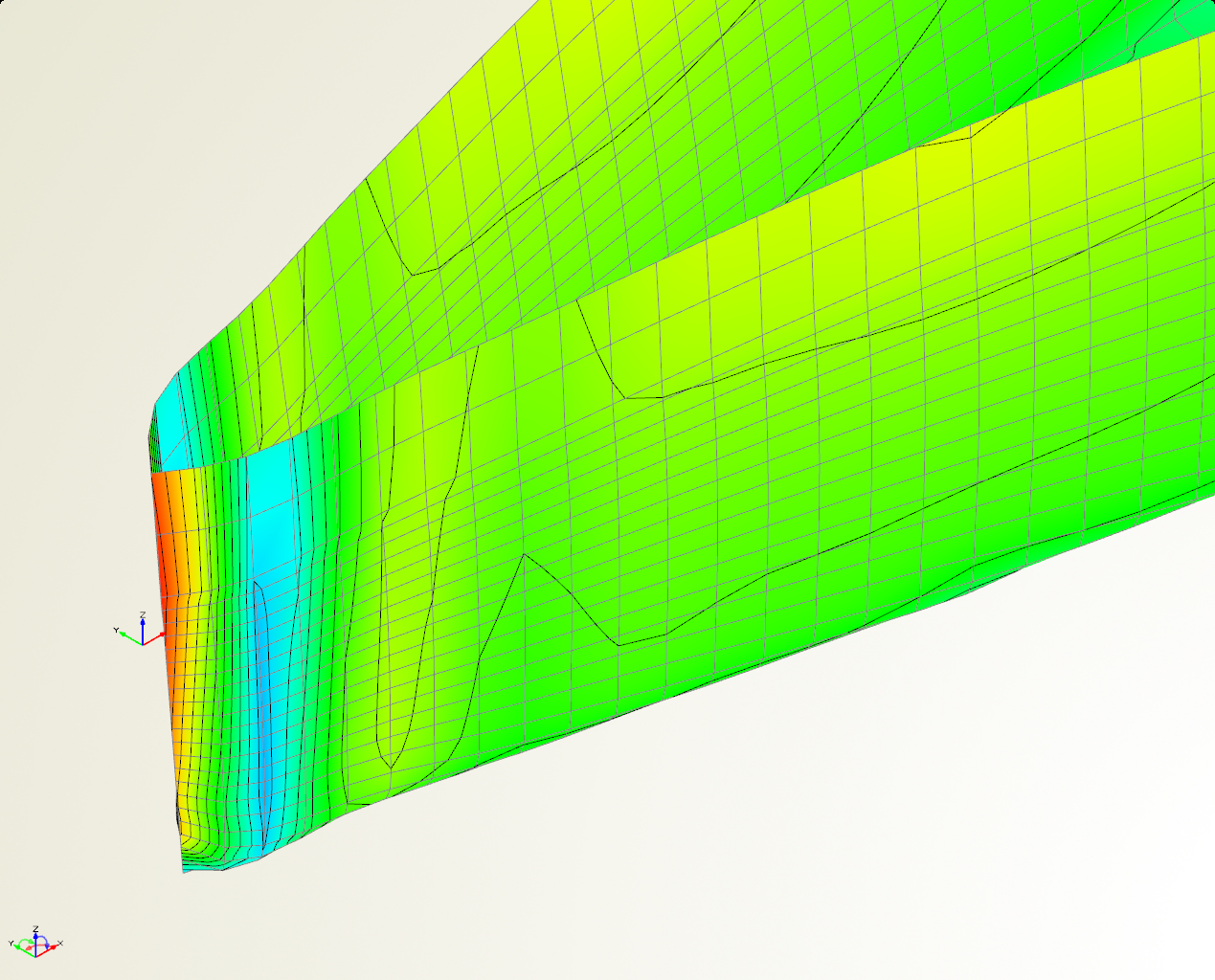
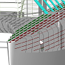
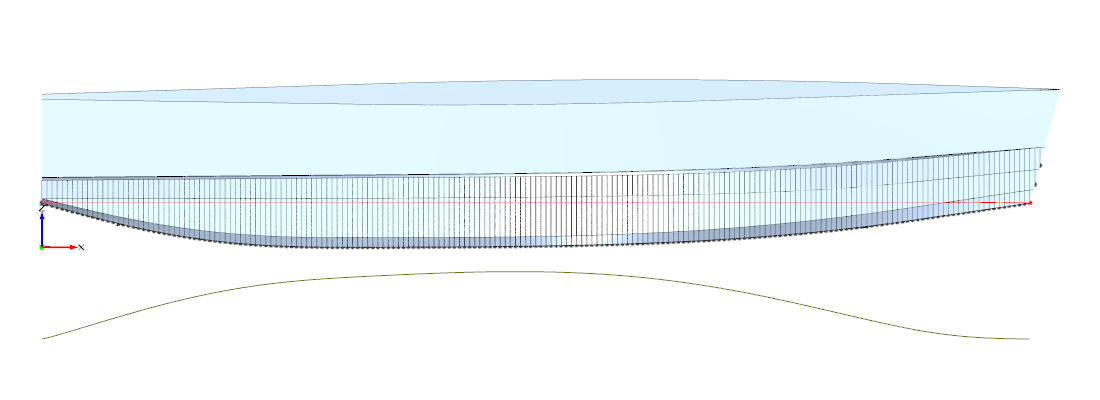
Abbildung 2: Netz am Bug (Buglinie, DENS 1,6)
Erste Untersuchungen ergaben, dass die Netze, die mit den Standard-Netzauflösungen "medium" und "fine" (letzteres entspricht D=1,0) erstellt wurden, im Bugbereich nur zu einem stark verzerrten Netz führen (vgl. Abbildung 1). Als kleinen Vorgriff sei an dieser Stelle auf die gestrichelte schwarze Kurve in Abbildung 4 verwiesen: Die Fehler in der Vernetzung schlagen sich auch als Ausreißer in der Kurve der Widerstandssbeiwerte nieder, die durch Integration des Druckes über die Rumpfoberfläche (CW) bestimmt werden. Die Netzqualität ist demnach von entscheidender Bedeutung für die Ergebnisse.
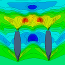
Als Ausweg wurde getestet, den Bug als separates Netz zu generieren, was zu recht ansehnlichen Netzen führt. Jedoch quittiert der Solver (XPAN) diese Vorgehen bei höheren Froudezahlen mit einem Fehler, weil das Bugnetz nicht mehr im Wasser ist. Hier sei angemerkt, dass alle Berechnungen in SHIPFLOW auf Spantkurven zur Definition der Rumpfform beruhen. Auf Grundlage des SHIPFLOW Handbuches, das sagt, das das Netz besonders regelmäßig wird, wenn der Bug als zentrale Bugline (stemline) vorgegeben wird, wurden die Spantkurven des runden Bugs durch eine Buglinie ersetzt. Leider zunächst ohne durchschlagenden Erfolg. Erst die Erhöhung der Netzauflösung von DENS=1,0 ("fine") auf mindestens DENS=1,6 führte wie von Geisterhand dazu, dass das Netz in dem Fall der Buglinie regelmäßig wurde (vgl. Abbildung 2). Weitere Untersuchungen ergaben, dass das Bugliniendesign recht anfällig ist für instabile Lösungen. Auch scheint dabei auf Grund der Geometrie eine senkrechte Vertiefung direkt hinter dem Bug zu entstehen, was an dem senkrechten blauen Bereich mit niedrigem Druck erkennbar ist. Dieser Effekt geht allerdings darauf zurück, wie ich die Bugline definiert habe. Somit wird der Bugbereich in diesem Fall eher schlecht nachgebildet. Schließlich wurde auf den durch Spanten definierten runden Bug zurückgegriffen. Das Netz dort sieht zwar auch nicht perfekt aus (vgl. Abbildung 3), aber die Ergebnisse konvergieren zuverlässiger als in den Fällen mit der Buglinie.
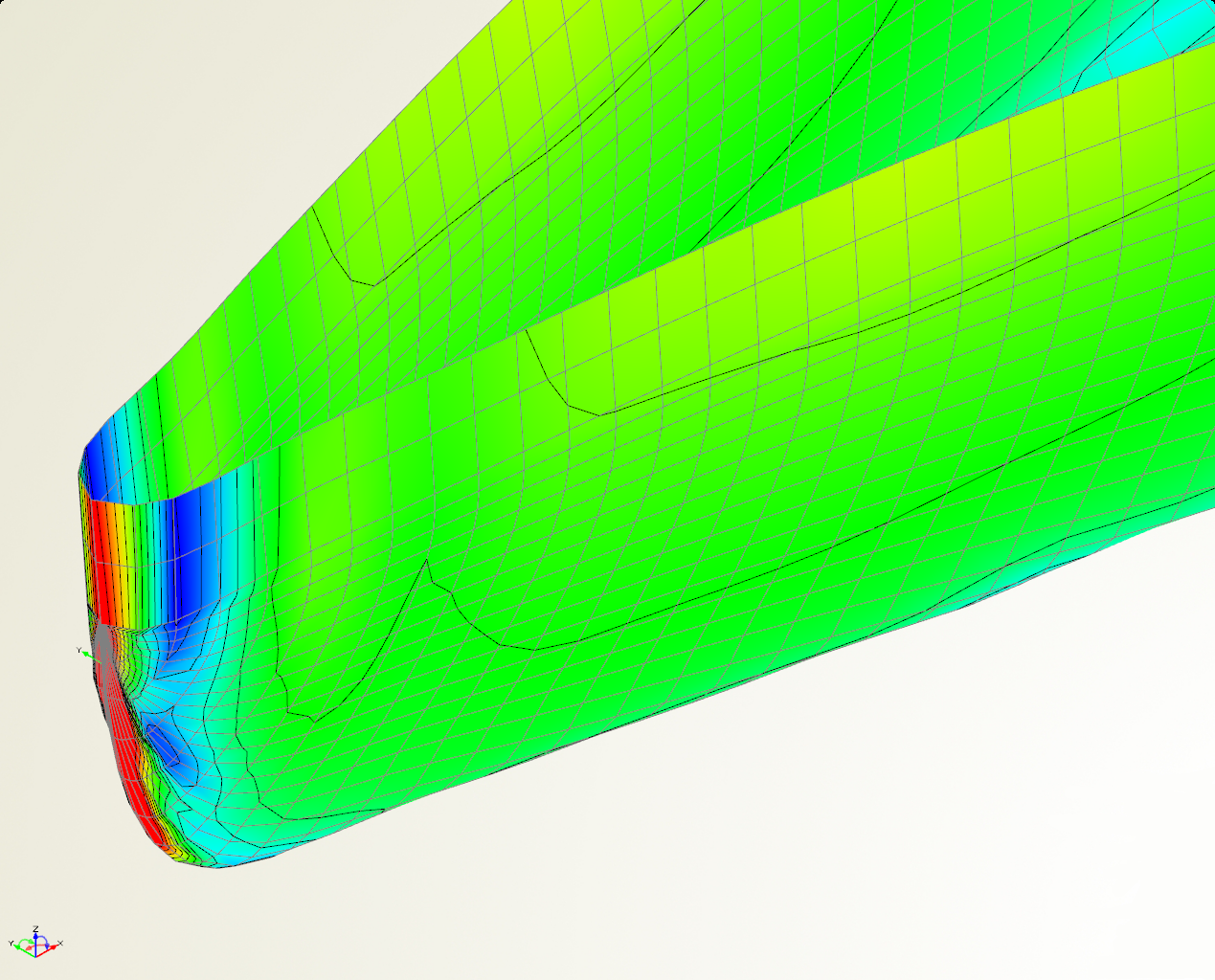
Abbildung 3: Netz am Bug (runder Bug, DENS 1,6)
Die Konvergenz der Berechnung, also nach wievielen Iterationen die berechneten Werte sich nur noch kaum verändern, ist auch ein wichtiges Thema. Dies trifft in besonderem Maße auf höhere Netzauflösungen zu, da dort jede Iteration verhältnismäßig lange dauert. Um die Konvergenz zu verbessern, wurde die Quellenrelaxation von Standardmäßig RELAX=0,7 auf 0,8 bis 0,9 erhöht. Der Effekt war durchweg positiv: Statt zum Teil bis zu 50 Iterationen oder gar keiner Konvergenz bei RELAX=0,7, sank die Zahl größtenteils auf weniger als 20 Iterationen, ohne dass sich dabei die Ergenisse messbar verändert hätten!
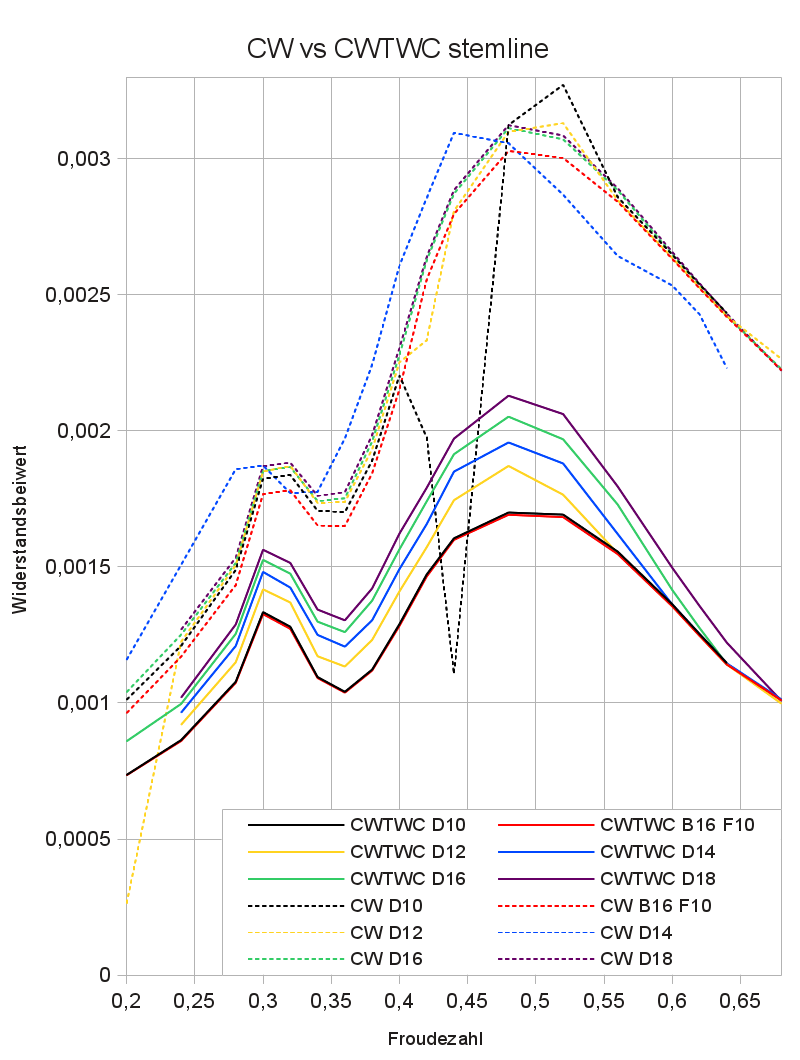
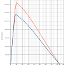
Abbildung 4: Widerstandbeiwerte (Buglinie)
Nach diesen Voruntersuchungen konnte ich mich der Betrachtung der Netzempfindlichkeit der Ergebnisse widmen:
Alle hier gezeigten Berechnungen wurden als nicht-lineare Berechnung der Wasseroberfläche und mit freiem Sink und Trim mit dem Modul XPAN von SHIPFLOW durchgeführt. Die Rechenzeit auf meinen Rechner (i7-3770k, 16 GB RAM) für eine Kurve mit 18 Punkten (d.h. 18 komplette CFD-Rechnungen) lag zwischen 45 Minuten für die geringste Auflösung und 11 Stunden und 20 Minuten für die Höchste Auflösung (allerdings nur 17 Werte, da $F_n$=0,2 wegen zu großem Speicherbedarfs (größer 8GB) nicht funktioniert hat). Für eine Optimierung ist es wichtig, dass sich der Rechenzeitbedarf in Grenzen hält. Dazu mehr an anderer Stelle.
Abbildung 4 vergleicht die Widerstandsbeiwerte, die über eine Intergration der Oberflächendrücke auf dem Rumpf berechnet wurden, CW, mit denen, die durch transversale Wellenschnitte (transversal wave cut), CWTWC, berechnet wurden. Die Netzauflösung wurde mit Hilfe eines Netzauflösungskoeffizienten "D"ens zwischen 1,0 und 1,8 variiert. Die Kurven bilden den gesamten mich interessierenden Bereich der Froudezahlen von $F_n$=0,2 bis $F_n$=0,68 ab. Die meisten Berechnungen wurden für gleiche Auflösungskoeffizienten für Rumpf ("B"ody) und Wasseroberfläche ("F"ree surface) durchgeführt, was durch den Koeffizient "D" angegeben wird. In einem Fall werden unterschiedliche Werte (B=1,6 und F=1,0) benutzt (s.u.). Die Netzausdehnung der Wasserfläche wird von SHIPFLOW automatisch auf Grundlage der Froudezahl bestimmt. Das bedeutet, dass die Ausdehnung zwar für alle Froudezahlen verschieden, aber für alle Netzauflösungskoeffizienten bei gleicher Froudezahl gleich sind. Dadurch ist sichergestellt, dass die einzelnen Werte nicht durch die Netzgröße beeinflusst werden. Versuche mit einer einheitlichen Netzgröße für alle Froudezahlen waren nicht sehr vielversprechend, aber das Thema habe ich noch nicht abschließend evaluiert.
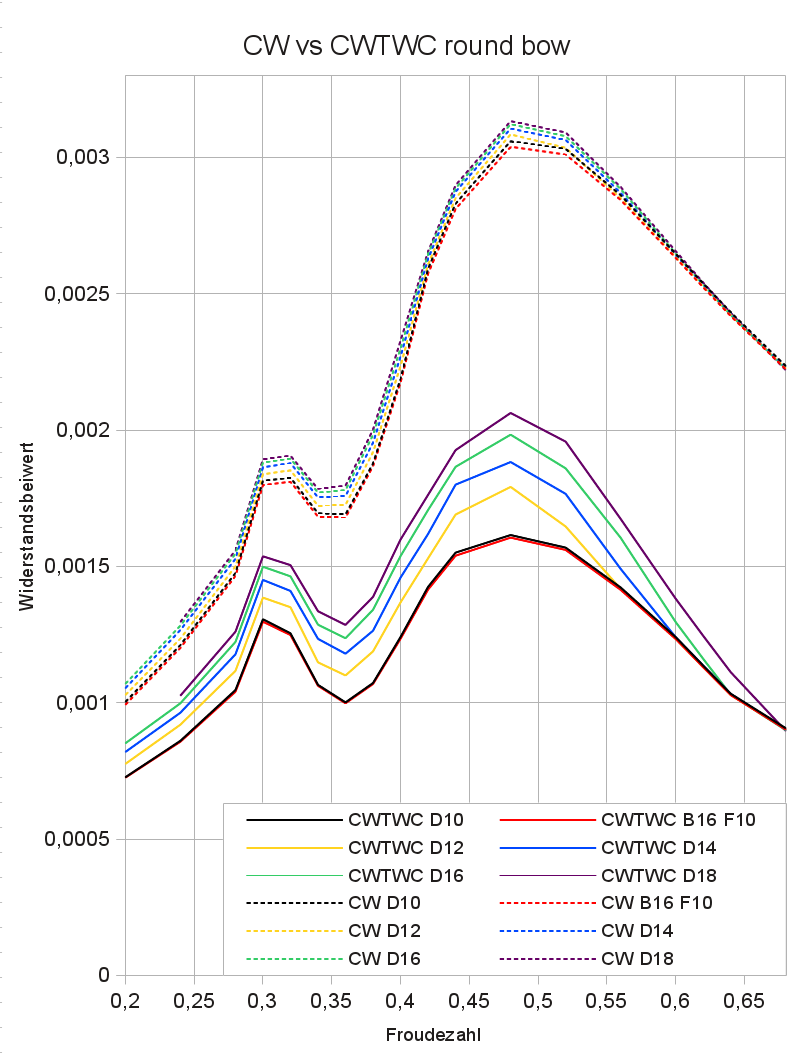
Abbildung 5: Widerstandsbeiwerte (runder Bug)
Besonders augenfällig ist, dass die CWTWC-Werte deutlich kleiner sind als die CW-Werte. Janson behauptet, dass die CWTWC-Werte näher an der Realität liegen. Das kann ich hier nicht überprüfen, allerdings ist diese Aussage zumindest bei meinem Design mehr als fragwürdig, weil die CWTWC-Werte mit zunehmender Netzauflösung kontinuierlich zunehmen. Über welchen Wert reden wir also? Der springende Punkt ist, dass die CWTWC-Werte hier nicht unabhängig von der Netzauflösung sind, sondern mit zunehmender Netzauflösung um über 30% zunehmen. Der einzige Lichtblick dabei ist, dass die Minima und Maxima der Kurven annähernd bei denselben Froudzahlen liegen. Bei den CW-Werten liegt ein anderes Problem vor: Bei Netzauflösungskoeffizienten bis 1,4 kommt es bei den CW-Werten immer wieder zu massiven Ausreißern, was darauf hindeutet, dass die Vernetzung dort fehlerhaft ist. Allerdings scheinen die Werte von den Ausreißern abgesehen weniger Fluktuation, also eine bessere Netzunabhängigkeit zu zeigen. Die zusätzlichen Kurven mit den Werten B=1,6 und F=1,0 wurden aufgenommen, um zu zeigen, dass der CWTWC-Wert tatsächlich nur von dem Netz der Wasseroberfläche und nicht von dem Netz des Rumpfes abhängt. Als Nebenergebnis zeigen diese Kurven auch, das CW auch von der Netzauflösung der Wasseroberfläche abhängt, da die CW-Kurven für D=1,6 (entspricht B=1,6 und F=1,6) bzw. B=1,6 und F=1,0 deutlich voneinander abweichen. Die Ausreißer, die bei D=1,0 auftreten, scheinen allerdings ausschließlich auf das Konto der Netzauflösung am Rumpf zu gehen.
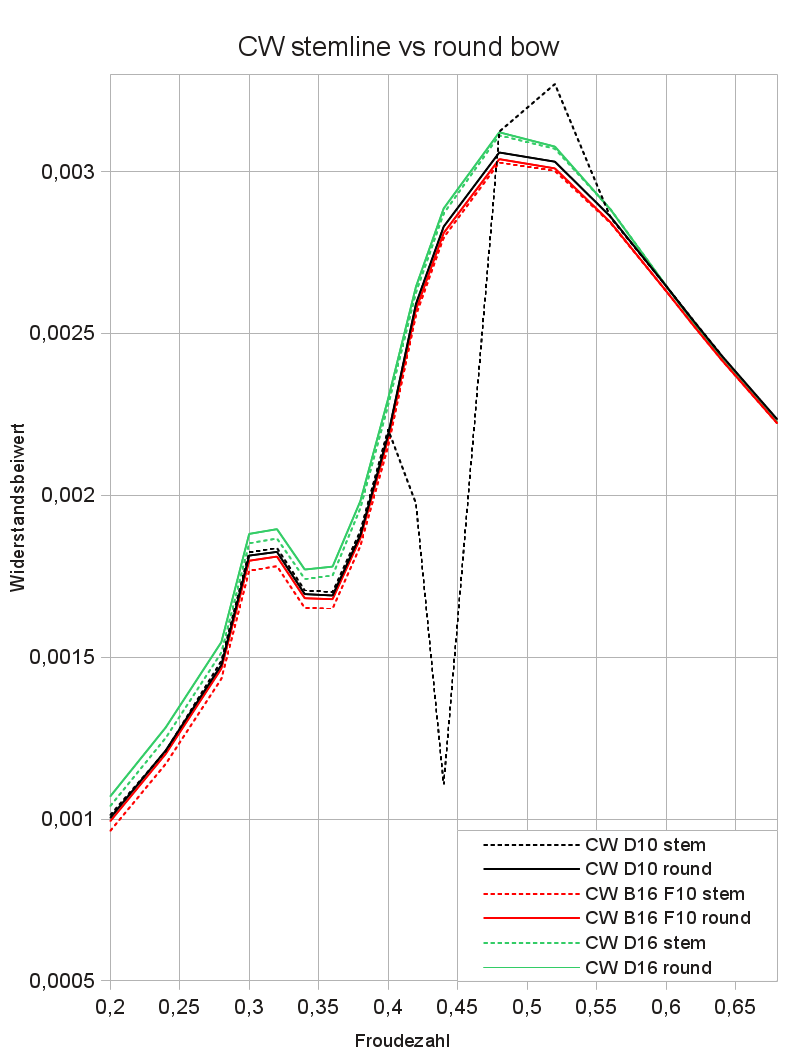
Abbildung 6:CW-Vergleich runder Bug vs Buglinienbug
In Abbildung 5 wurden dieselben Berechnungen wie in Abbildung 4 durchgeführt, wobei jedoch ein direkt durch die Spanten definierter runder Bug verwendet wurde. Als erstes fällt auf, dass es hier keine Ausreißer gibt, was für eine Optimierung vorteilhaft ist. Ansonsten zeigt sich ein ähnliches Bild wie in Abbildung 4: Die CWTWC-Werte zeigen eine starke Netzabhängigkeit, die CW-Werte eine deutlich geringere. Bei CWTWC liegt die Zunahme von D=1,0 nach D=1,8 bei maximal 29,4%, bei CW nur bei 6,6%. Ab einer Netzauflösung von D=1,4 nehmen die CW-Werte nur noch um maximal 2,6% zu, was auf einen fixen Grenzwert hindeutet.
In Abbildung 6 schließlich wurde analysiert, ob der runde Bug im Widerstandsbeiwert von dem Bug mit der Bugline abweicht. Dabei liegen die Werte für den Buglinien-Bug meist geringfügig unter denen des runden Buges. Ob das einen tatsächlichen Widerstandsvorteil zeigt oder auf Rechenungenauigkeiten zurückgeht, kann hier nicht entschieden werden: Im interessantesten Bereich von $F_n$=0,3 bis 0,5 weichen die Werte um maximal 1,67% voneinander ab, was durchaus auf die unterschiedliche Vernetzung zurückzuführen sein kann.

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998