02.03.2015
Numeca Fine/Marine Tests
Eine Frage, die mich schon lange umtreibt ist: Bewegen sich die Ergebnisse, die
ich mit SHIPFLOW berechnet habe, annähernd in einem realistischen Bereich oder sind
das alles nur Fantasiewerte ohne Realitätsbezug?
Wissenschaftlich gesehen ist das der Schritt, wo man
versucht durch andere Methoden seine Ergebnisse zu plausibilisieren. Logisch wäre ein
Tanktest, aber das ist natürlich zu aufwendig. Daher habe ich die Gelegenheit
wahrgenommen, von NUMECA eine 30 Tage Testlizenz zu bekommen, um ein paar Testrechnungen
zu machen.
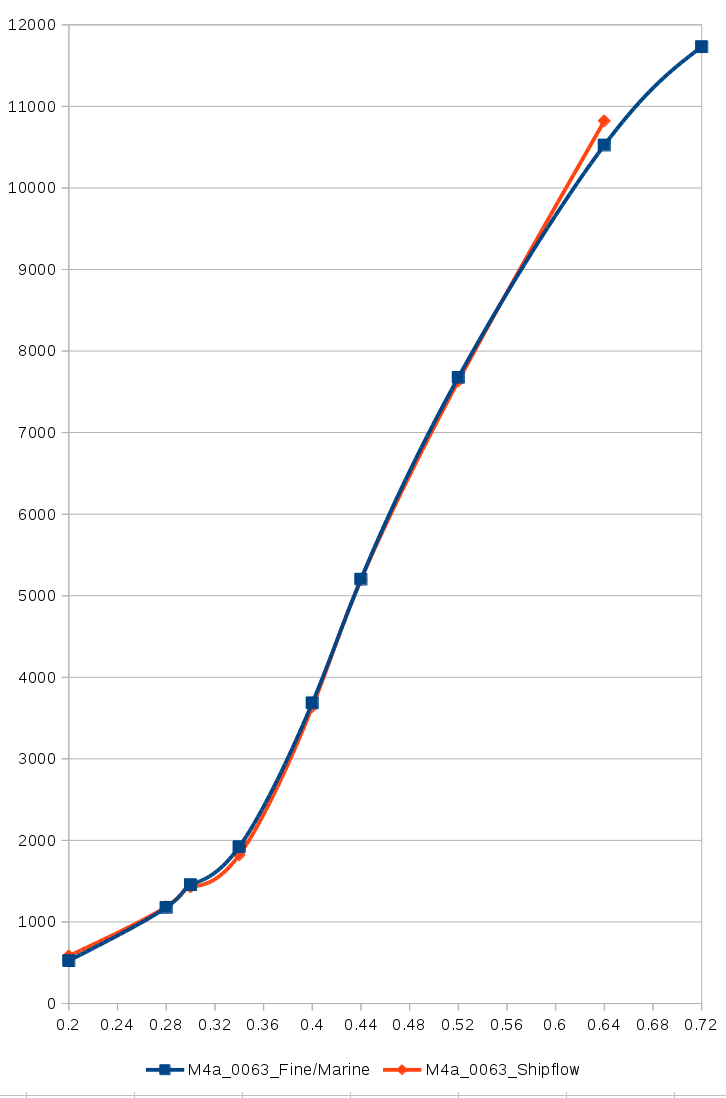
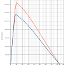
Abb. 1: Gesamtwiderstand SHIPFLOW vs. Fine/Marine
Kurz gesagt: Die Ergebnisse liegen so gut beieinander, dass ich mir keine Sorgen
machen muss. Abbildung 1 zeigt die Gesamtwiderstandskurven des Modells M4a_0063 im
Vergleich von SHIPFLOW versus Fine/Marine für einen Rumpf mit den selben
hydrodynamischen Parametern für Salzwasser. Es sieht so aus, als bewegte ich mich
von ein paar Ausreißern abgesehen im Bereich von etwa 1-3% Abweichung zwischen den zwei
Programmen. Gerade im Bereich des ersten Widerstandsbergs ($F_n=0.30$) scheint es keine
bösen Überraschungen zu geben. Das ist wichtig weil das mein Hauptauswahlkriterium war.
Die Programme arbeiten aber mit vollkommen verschiedenen Ansätzen:
SHIPFLOW mit dem zonal approach
(Panelmethode mit VOF-Berechnung
im Heckbereich) und Fine/Marine mit einem kompletten VOF-Ansatz zum Lösen der
Navier-Stokes-Gleichungen in 3D inklusive Wellenoberfläche.
Allerdings möchte ich mich hier einem anderen Thema zuwenden, nämlich der Frage,
welchen Einfluss eine Katamarankonfiguration im Gegensatz zu einer Ein-Rumpf-Simulation
auf den Gesamtwiderstand hat. Bei den Pi-mal-Daumen
-Überlegungen für Blu:Kat wurde
behauptet, dass der Einfluss vernachlässigbar sei. Ich konnte mit Fine/Marine
nachweisen, dass das nur die halbe Wahrheit ist: Bei geringen Geschwindigkeiten
($F_n=0.30$ (ca. 8 Knoten)) trifft das bei meinem Rumpf einigermaßen zu,
bei höheren Geschwindigkeiten
($F_n=0.44$ (ca. 12 Knoten)) definitiv nicht (vgl. Tabelle 1).
| Foude/Bezeichnung | Ein Rumpf | Katamaran (BCB=4,25m) | $\Delta_R$ |
|---|---|---|---|
| $F_n = 0.30$ | 2872 | 2908 | +1,3% |
| $F_n = 0.44$ | 10568 | 12506 | +18,3% |
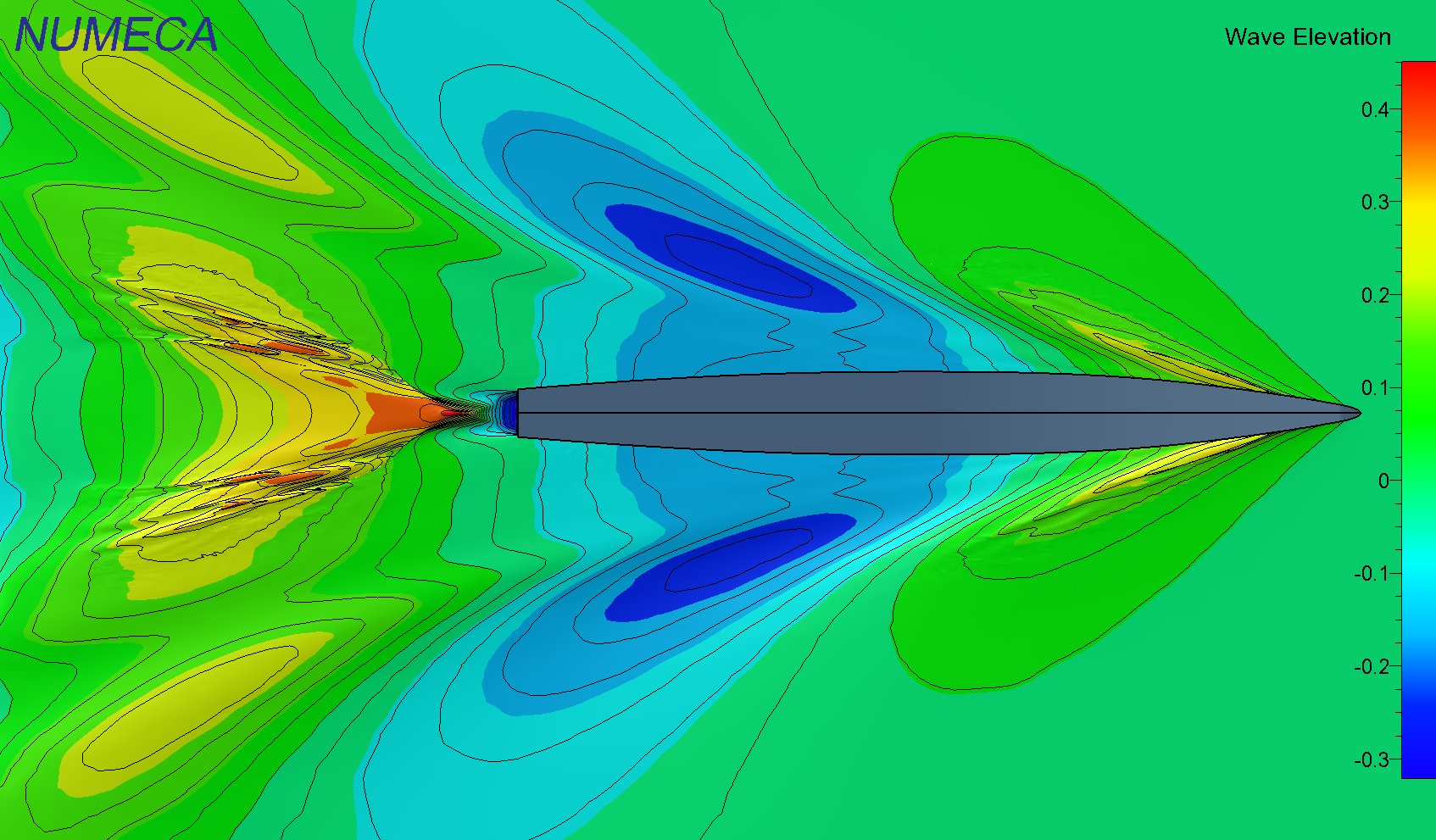
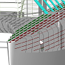
Abbildung 2: Wellenbild für einen Rumpf
Abbildungen 2 und 3 zeigen die Wellenbilder für einen einzelnen Rumpf bzw. eine Katamarankonfiguration. Die Rumpfform ($LWL=20,17m$, $BWL=1,85m$) und die Geschwindigkeit ($F_n = 0,44$) sind in beiden Fällen gleich. Das Maß BCB bezeichnet den Abstand zwischen Mittschiffslinie und Mittellinie eines Rumpfes (Schwimmers). Am Wellenbild für die Ein-Rumpf-Simulation und der Katamaran-Simulation ist gut erkennen, woher der zusätzliche Widerstand kommt: Die Wellen überlagen sich mittig zwischen den Rümpfen, einmal als Vertiefung zwischen den Rümpfen (blau) und einmal als vergrößerte Heckwelle mittig hinter den Rümpfen (gelb/orange/rot).

Abbildung 3: Wellenbild Katamaran (BCB=4,25m)
Eine solche Heckwelle kann bei höheren Geschwindigkeit erhebliche Dimensionen annehmen und so maßgeblich zum Gesamtwiderstandbeitragen. Eindrucksvoll zu erkennen ist eine solche Welle z.B. bei der Katamaran-Schnellfähre nach Stewart Island (Neuseeland) ($LWL = 25m$, $F_n = 0,83$ (25 Knoten)). Diese Welle erreicht geschätzt bis zu zwei Meter Höhe (vgl. Abbildung 4).

Abbildung 4: Heckwelle ($F_n = 0,83$)
In Anbetracht die dieser Rumpfintereferenzen stellt sich die Frage, wie
man diesen Widerstand reduzieren kann. Die naheliegende Antwort ist eine Vergrößerung
des Abstandes zwischen den Rümpfen. Tabelle 2 zeigt diesen Effekt für verschiedene BCB.
Die Frage, die bleibt, ist, ob und wie man die Größe der Heckwelle mit der Rumpfform
beeinflussen kann. Die Studienarbeit
Design and optimization of a 50' sailing catamaran
von Perret beschäftigt sich mit
dieser Frage. Demnach scheint es möglich zu sein, die Heckwelle zu reduzieren, indem
die Rumpfunterseite am Heck in der Seitenansicht leicht konkav gestaltet wird. Allerdings
funktioniert das mit meiner Knickspantbauweise nicht ordentlich. Ferner hat demnach
auch die Hecktauchtiefe einen Einfluss auf den Widerstand. Allerdings bewegt sich
der untersuchte Geschwindigkeitsbereich dort im Bereich $F_n = 0,4...0,7$. Die
Strafe
, die man für diese Maßnahmen im niedrigen Geschwindigkeitsbereich
bezahlt, wird dort also nicht sichtbar. Beipielsweise führt eine tiefere Hecktauchung
zu mehr Totwasser, was den Widerstand in diesem Bereich erhöht.
Ein weiterer Schwachpunkt der Studienarbeit
ist, dass das verdrängte Volumen nicht exakt konstant gehalten wird, was an der manuellen
Generierung der Modelle mit Rhino liegt. Es ist also fraglich, ob die Ergebnisse nicht
zumindest teilweise auf das Konto der Verdrängungsänderung gehen.
Die Erklärung, wieso es zu der Reduktion des (Wellen-)Widerstands kommt, ist einfach: Die konkave Form sorgt in diesem Geschwindigkeitsbereich bereits für leichten hydrodynamischen Auftrieb am Heck, was die Vertrimmung reduziert. Ein Rumpf der weniger vertrimmt hat aber grundsätzlich einen geringeren Wellenwiderstand, wie ich in meinen Untersuchungen bestätigen konnte. Für mich bedeutet das, dass Heckkonfigurationen, die gerade oder mit minimaler Konvexität auslaufen, das erreichbare Minimum darstellen.
| BCB [m] | Gesamtwiderstand [N] | $\Delta_R$ (bezogen auf BCB=4,0m) |
|---|---|---|
| 4,00 | 12908 | 0,0% |
| 4,25 | 12506 | -3,10% |
| 4,50 | 12258 | -5,0% |

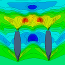
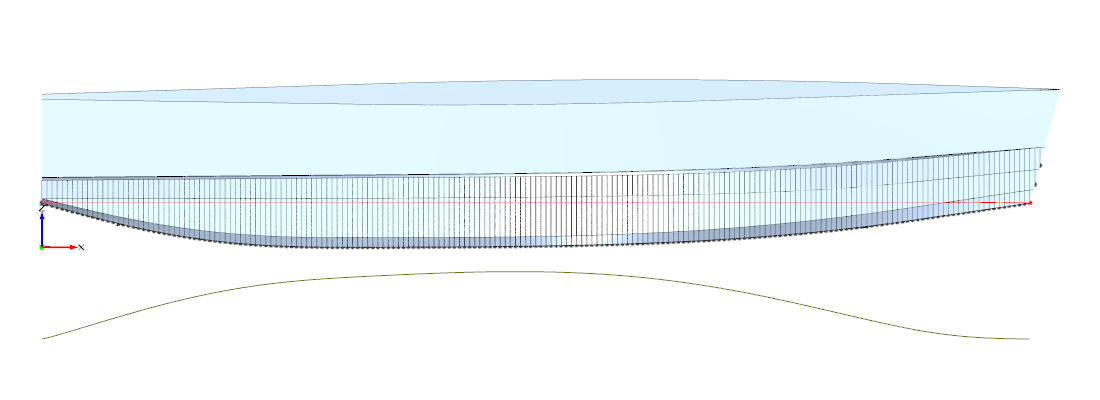
Abbildung 5: Abrisskante ($F_n = 0,30$)
Eine weitere Frage, die ich aus Zeitmangel nur ansatzweise untersucht habe, ist die Frage, die ich bereits unter dem Menüpunkt CFD/SHIPFLOW (potential flow) theoretisch zu erörtern versucht habe, nämlich die Frage, ab welcher Geschwindigkeit das Wasser bei welcher Hecktauchung am Heckspiegel sauber abreißt. Die Fine/Marine Simulation hat gezeigt, dass die Strömung bei $F_n = 0,30$ (8 Knoten) und einer Hecktauchung von 7,5 cm bei meinem Design sauber abreißt. Weitere Untersuchungen für niedrigere Geschwindigkeiten fehlen mir leider. Abbildung 5 zeigt die Heckpartie für $F_n=0,30$. Die leuchtend grüne Line zeigt den Verlauf der aktuellen Wasserlinie. Sie folgt der Geometrie des Rumpfes.

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998