31.10.2014
Parametrisches Modell 3
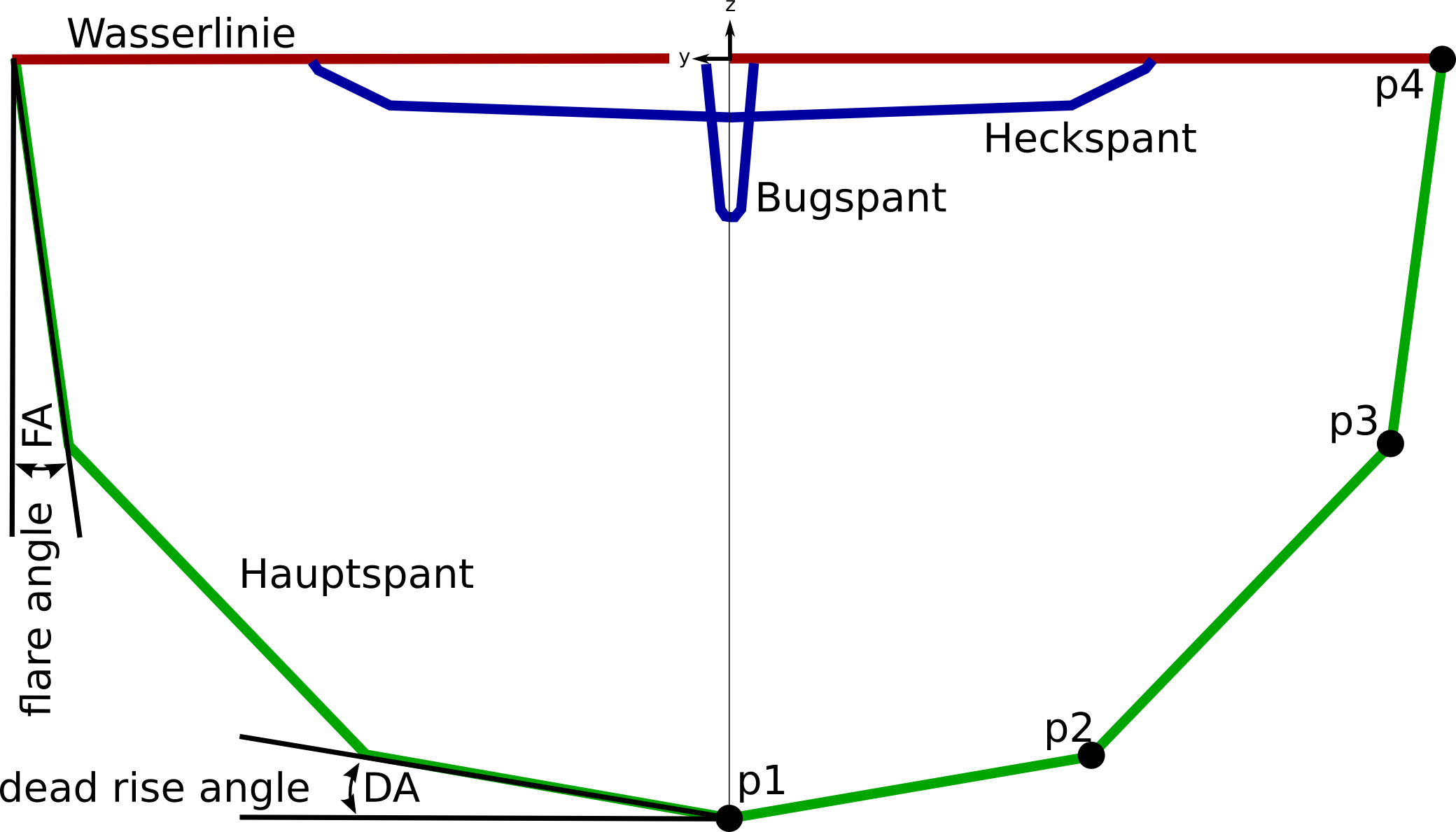
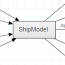
Abbildung 1: Geometrie des Modells 3
Nachdem das Modell 2 gezeigt hatte, dass eine Vielzahl von Spanten nicht zu glatten Knickkurven führt, beschreitet Modell 3 den entgegengesetzten Weg: Es gibt nur noch drei vordefinierte Spanten: Einen Heckspant, einen Hauptspant und einen Bugspant. Die Knicke dieser Spanten werden wie gewohnt mit CSplines verbunden. Klar ist, dass man damit die Verdrängung nicht mehr direkt via Spantflächenkurve vorgeben kann. Da es aber immer mein Ziel war, von der Verdrängung her nur exakt gleiche Designs zu vergleichen, wird dies in diesem Modell durch eine Optimierungsrechnung erreicht: Die Spantfläche des Hauptspants (und auch der anderen) kann direkt vorgegeben werden. Mit Hilfe des Brent-Minimierers des Friendship-Frameworks wird die aktuelle Verdrängung, die direkt von der Hauptspantfläche abhängt, solange variiert, bis die aktuelle Verdrängung dem Zielwert entspricht.
Bestimmen der Spantflächengeometrie
Auf Grundlage der geometrischen Verhältnisse bei zwei Knicken im Unterwasserbereich läßt
sich unter Vorgabe von dead rise angle (DA), flare angle (FA) (vgl. Abbildung 1) und der
Spantfläche unter zu Hilfenahme der Spantkurvenlänge ein mathematischer Ausdruck
für die Lage der Knickpunkte p2 und p3
in Form einer quadratischen Gleichung aufstellen, die man direkt nach den interessierenden
Punktkkoordinaten von p2 und p3 auflösen kann.
Das wäre so ein typischer Fall
für einen Professor an einer Uni zu sagen "Wie man leicht sieht..". Nein, man sieht
nicht leicht, auch wenn es nur eine quadratische Gleichung ist:
Diese ist eher länglich und die Rechnung beansprucht etwa zwei
DINA4-Seiten, nachdem man vorher das Koorinatensystem sauber definiert hat. Sorry, aber
diesen Seitenhieb konnte ich mir leider nicht verkneifen.)
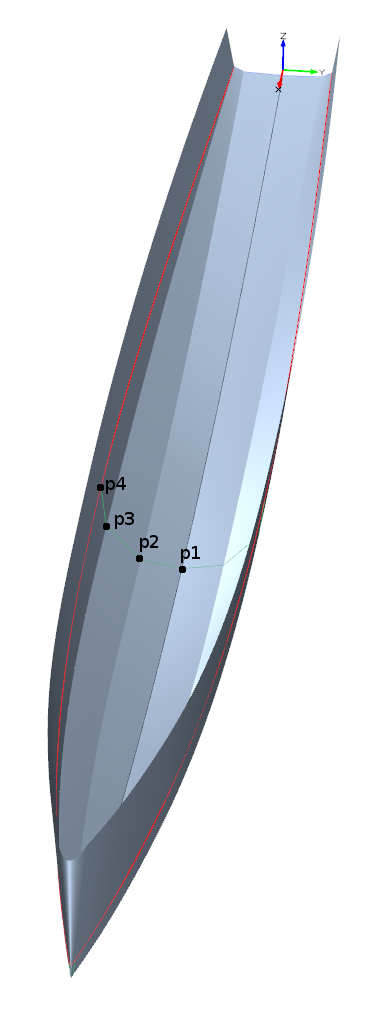
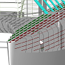
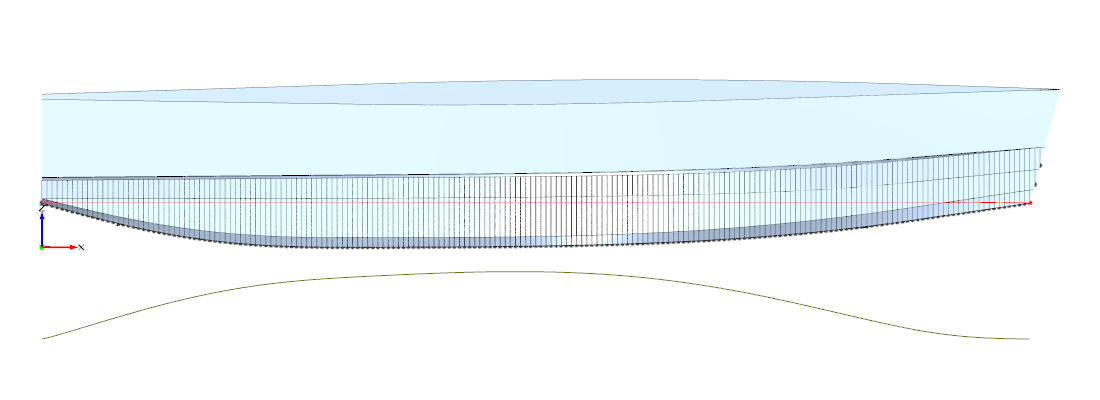
Abbildung 2: Beispiel eines generierten Modells 3
Zusätzlich verfolgt dieses Modell auch einen Ansatz, die benetzte Fläche so gering wie möglich zu halten, da sich diese direkt auf den Reibungswiderstand auswirkt: Die Idee dabei ist, dass die Kantenlänge der Spantkontur minimmiert wird. Ist diese Länge bei gegebener Spantfläche minimal, ist auch die benetzte Fläche im Rahmen dieser Annahme minimal. Deshalb habe ich sie bei der Bestimmung der quadratischen Gleichung eingesetzt, um ein vollständig bestimmtes Gleichungssystem zu erhalten. Ich hätte auch den Seitenwinkel direkt vorgeben können (war ehrlich gesagt der erste Ansatz), aber dann hätte ich den Vorteil der minimalen Spantkurvenlänge verloren. Beispielrechnungen haben gezeigt, dass es kaum möglich ist, Knickspant-Rümpfe mit geringer benetzter Fläche zu konstruieren, als die mit diesem Verfahren bestimmten.
Die Längsachenposition (x-Achse) der Hauptspantfläche ist frei wählbar, so dass ich die Lage des Verdrängungsschwerpunktes beeinflussen kann. Unabhängig davon kann auch die x-Lage des tiefsten Punktes der Mittschiffsline (centerline, CL) festgelegt werden. An diesem Punkt wird eine waagerechte Tangente als zusätzliche Bedingung für die CL-Kurve festgelegt, damit der teifste Punkt auch tatsächlich dort liegt. Gleiches gilt auch für die größte Breite der Wasserlinenkurve (WL). Diese beiden Kurven stellen gleichzeitig auch Parameterkurven für die Spanten dar: Wird ein Spant an einer gegebenen x-Position definiert, dann definieren der Tiefgang der CL und die Breite der Wasserline an dieser Stelle die Koordinaten der Punkte p1 und p4.
Zusätzlich kann ich die Spitzheit der Wasserlinienkurve am Bug und die Breite am Heck direkt vorgeben. Es hat sich gezeigt, dass besonders die Spitzheit des Buges einen extremen Einfluss auf den Wellenwiderstand hat.
Um den Hauptspant entlang der Schiffslänge ohne ständiges Anpassen oder Vorgabe von DA und FA verschieben zu können, wurden Parameterkurven für DA und FA über die gesamte Schiffslänge definiert. Diese Werte gehen direkt in die oben genannte quadratische Gleichung ein, um die Lage von p2 und p3 zu bestimmen. Der Winkel des mittleren Segments (zwischen p2 und p3) ist bei dieser Rechnung noch unbestimmt, beeinflusst aber maßgeblich die Länge der Spantline. Um diesen Parameter festzulegen, wird auf die oben erwähnte Minimierung der Länge der Spantline zurückgegriffen, um diesen freien Parameter optimal zu nutzen.
Es soll nicht unerwähnt bleiben, dass die Fläche zwischen p3 und p4 gradlinig über die Wasseroberfläche hinaus verlängert wird (vgl. Abbildung 2), um nicht einen strömungstechnisch ungünstigen zusätzlichen Knick direkt an der Wasserlinie zu erzeugen. Damit dies zu keinen unerwarteten Dellen und Beulen führt, mußte ich darauf achten, dass sich die Knickkurven durch p3 und die durch p4 geometrisch ähneln, also in y- und z-Richtung ähnliche Krümmungen aufweisen. Im Bugbereich mußte ich dazu mit Hilfe eines zusätzlichen Stützpunktes eingreifen, sonst wären die Büge abstrus füllig geworden.
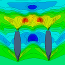
Das Modell funktioniert in weiten Parameterbereichen. Die so generierten Rumpfformen haben alle glatte ("strakende") Knickkurven und bilden daher eine gute Grundlage für die Simulationen mit SHIPFLOW (vgl. Abbildung 2). Allerdings kann es vorkommen, dass ein Spant die Vorgabewerte für DA, FA, Spantfläche, Tiefgang, Wasserlinienbreite und Verdrängung nicht erfüllen kann. In diesem Fall "entartet" das Modell komplett und ist ein Fall für den Mülleimer. Aus diesem Grund generiere ich zuerst nur valide Modelle und füttere sich dann in die Simulation ein. Das war bis Version 3.1 des Friendship-Frameworks etwas mühsam (vgl. den entsprechenden Blog bei Friendship-Systems), aber seit dieser Version kann man beliebige Parameterkombinationen direkt in einen sogenannten "Designassembler" als CSV-Datei importieren und in die CFD-Simulation füttern.
Darüber hinaus existiert noch ein Modell 3c (3a und 3b waren korrigierte Versionen des Grundmodells), dass sich von Modell 3 dadurch unterscheidet, dass man Spanthöhe und Eintauchtiefe der Spanten an Bug und Heck frei vorgeben kann. Genutzt wird diese Eigenschaft, um auch Modelle generieren zu können, die ein "normales" Yachtheck im Gegesatz zu dem bisher verwendeten Spiegelheck (transom stern) haben. Das Problem dabei liegt in der Simulation: Spiegelhecks werden in SHIPFLOW anders vernetzt als Yachthecks. Eine direkte Vergleichbarkeit ist somit schwierig.

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998