08.07.2022
Die Vektorsteuerung
Im Yachtbereich ist man sehr den Traditionen verhaftet, was oftmals zu unnötig komplizierten Lösungen führt. Dies trifft im Besonderen auf Katamarane zu: Da diese Bootsform in weiten Teilen der Welt, so auch in Europa, keine lange Geschichte haben, werden regelmäßig Konzepte von Einrumpfbooten in verdoppelter Form auf Katamarane übertragen. So auch das Antriebskonzept für größere Segelkatamarane: Es werden zwei Hauptantriebe am Heck und zwei Bugstrahlruder installiert, obwohl es zumindest in der Theorie ein Leichtes ist, ein Schiff, dass zwei weit voneinander entfernte Antriebe aufweist, in jede beliebige Richtung zu manövrieren. Sofern die Antriebe um 360° drehbar sind, können sie als ein einziger Vektorantrieb konzipiert und angesteuert werden, der jeden beliebigen Schubvektor bereitstellen kann. Gerade bei einem Segelkatamaran lässt sich durch den Entfall der Bugstrahlruder die Segelperformanz verbessern – von den eingesparten Rumpfdurchbrüchen ganz zu schweigen.
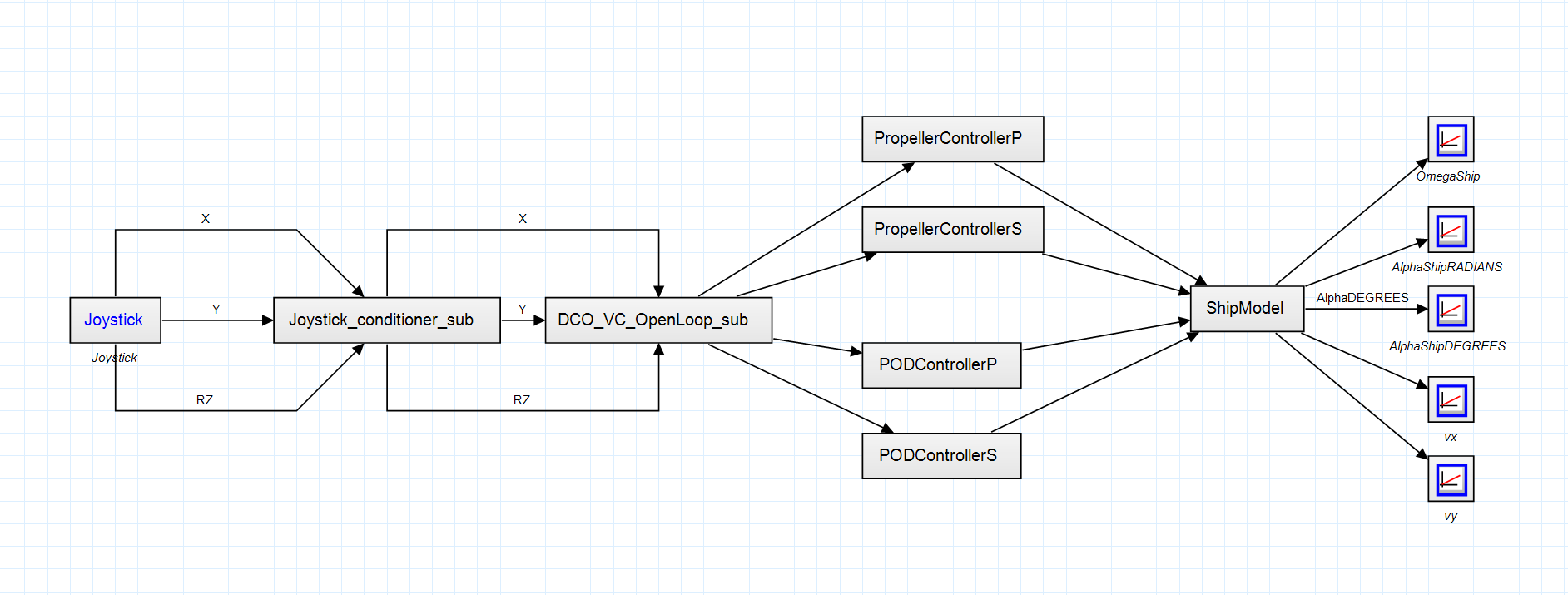
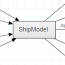
Abbildung 1: Schema der Vektorsteuerung
Modellbildung
Eine solchen Ansatz habe ich für die DreamCatcherOne umgesetzt und am 1:10 Modell
getestet. Die Herausforderung ist, die Steuerbefehle in X, Y und RZ (Drehung des Joysticks)
in Drehzahl und Podwinkel der beiden Podantriebe umzusetzen.
Dabei bin ich in zwei Schritten vorgegangen: Zunächst habe ich mit der Simulationsumgebung
20sim ein Modell des Katamaran entwickelt und dieses dann mit einem von mir entwickelten
Steuer- und Regelkonzept betrieben. Dabei habe ich einen normalen Joystick aus dem
Computerspielebereich genutzt und aufgezeichnet, wie sich das simulierte Schiffsmodell
hinsichtlich Vorwärts-, Seitwärts- und Rotationsbewegungen verhält. Zunächst habe ich ein
reines Steuerverfahren getestet, das kein Feedback der Schiffsbewegungen verwendet.
In einem zweiten Schritt habe ich den Regelkreis geschlossen, so dass unerwünschte
Drehbewegungen, die dem Steuersystem inhärent sind, ausgeregelt werden können.
In der Praxis verlangt dies einen Gyrosensor.
Abbildung 1 zeigt den prinzipiellen Aufbau des Steuersystems ohne Feedback.
Das Simulationsmodell liest die Befehle vom Joystick ein, normiert sie auf den Bereich
[0.0 .. 1.0] und passt die Achsen so an, dass ein Nachvorneschieben des Joysticks auch
eine Vorwärtsbewegung des Katamarans auslöst (Joystick_conditioner). Die eigentliche
Magie
passiert in dem Modul DCO_VC_OpenLoop
: Hier werden die
Joystickauslenkungen in Steuerbefehle für die PropellerControllerP/S
und die
POSControllerP/S
umgesetzt. Die genannten Controller umfassen in der Simulation natürlich
nicht nur die Regler, sondern auch die Modelle der Strecken. Am Beispiel der Drehzahl des
Podantriebs lässt sich die Modellierung wie folgt veranschaulichen:
Das Modell für den drehzahlgeregelten Antrieb basiert in der Regel auf einem Modell des Umrichters, einem elektrischen Modell des Motors, sowie einem mechanischen Modell des Motors. Leicht vereinfacht würde man dabei eine $PT_{3}$-Strecke erhalten, wobei die Totzeit $T_{t}$ und die Spannungsverstärkung $K_{sp}$ des Umrichters als $PT_{1}$ Glied eingehen und der Verstärkungsfaktor des Drehzahlsensors $K_{s}$ berücksichtigt wird. Diese Strecke wird aber so weiter vereinfacht, dass die Zeitkonstanten und Verstärkungsfaktoren des elektrischen Teils (Drehzahlsensor, Umrichter und Motor) in je einer Konstanten zusammengefasst werden, so dass ein vereinfachtes $PT_{2}$-Streckenmodell entsteht, das nur noch aus einem Sammel-$PT_{1}$-Glied für alle elektrischen Komponenten und einem Sammel-$PT_{1}$-Glied für alle für alle mechanischen Komponenten (Trägheiten von Motor, Getriebe und Schiffschraube).
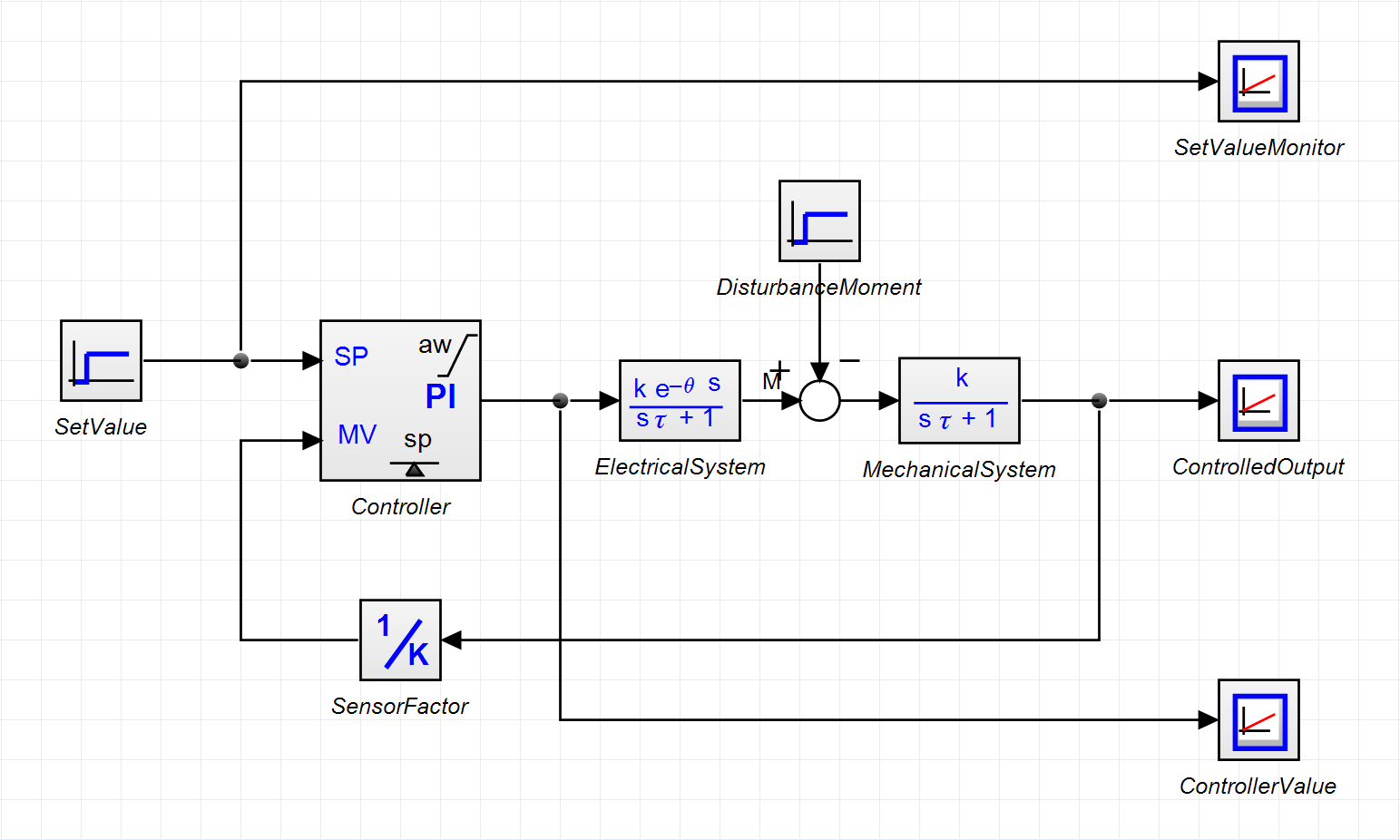
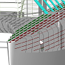
Abbildung 2: Schema der Poddrehzahlregelung
Dies ist deshalb möglich weil $T_{M} \ll \sum_{i} T_{i}$, wobei $T_{M}$ die mechanischen Zeitkonstanten beschreibt und $T_{i}$ die elektrischen von Umrichter und Motor. Somit gilt für den Ersatzverstärkungsfaktor des elektrischen Teils $K_{ES} = K_{s} \cdot K_{sp} \cdot K_{a} \cdot K_{MMot}$, wobei $K_{a} = \frac{I_{A}(t\to\infty)}{U_{a0}}$ die Antriebsverstärkung bei Nennspannung $U_{a0}$ und $K_{MMot} =\frac{M_{m0}}{I_{a0}}$ die Momentenkontante des Motors bei Nennmoment $M_{m0}$ und Nennstrom $I_{a0}$ ist. Für die Ersatzzeitkonstante ergibt sich $T_{ES} = T_{t} + T_{a}$ wobei $T_{a}$ die elektrische Zeitkonstante des Motors (basierend auf der Induktivität der Wicklung) ist. Für den mechanischen Teil geht man von der Momentengleichung einer Rotations bewegung aus, also \begin{equation} \label{eq:Mmoment} J_{Ges} \cdot \frac{d\omega(t)}{dt} = M_{M}(t) - M_{R}(t) - M_{L}(t) \end{equation} wobei $M_{M}(t)$ das Antriebsmoment des Motors ist, $M_{R}(t) = r_{k} \cdot \omega(t)$ das Reibungsmoment mit dem Reibungskoeffizienten $r_{k}$ ist und $M_{L}(t)$ das Lastmoment, das wird nicht kennen und daher vernachlässigen. Auf $PT_{1}$ Normalform $T{M} \cdot \frac{d\omega(t)}{dt} + \omega(t) = K{M} \cdot M_{M}(t)$ gebracht, ergeben sich die Parameter der mechanische Strecke zu \begin{equation} \label{eq:Mkonstants} K_{M} = \frac{1}{r_{k}} \left[\frac{s^{-1}}{Nm}\right], \quad T_{M} = \frac{J_{Ges}}{r_{k}} \left[s\right] \end{equation} Dabei berücksichtigt die Gleichung nur die Gleitreibung, die proportional zur Drehzahl ist. Statische Haftreibung und Coulomb-Reibung werden in dem vereinfachten Modell vernachlässigt. Die Zeitkonstante $T_{M}$ lässt sich aus der Sprungantwort einfach gewinnen. Bei hinreichender zeitlicher Auflösung der Messung sollte man da auch die Ersatzzeitkonstante $T_{ES}$ ablesen lassen, das diese im vereinfachten Modell der Totzeit des Umrichters entspricht ($T_{ES} \approx T_{t}$). Steuert man den Umrichter mit Hilfe eines Signalgenerators an und triggert auf den Einschaltpunkt, dann sollte $T_{t}$ dem Abstand zwischen Einschaltzeitpunkt und dem beginnenden Drehzahlanstieg sein. Das Ganze steht und fällt damit, ob man die Drehzahl akurat erfassen kann oder nicht. In der Simulationsumgebung 20sim sieht das Ganze dann wie in Abbildung 2 aus.

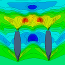
Abbildung 3: Simulationsmodell des Schiffs
Für die Praxis ist es wichtig, dass auch in dem Modell die Propellerdrehzahlen tatsächlich geregelt sind, weil die Steuerbefehle für den Modellbaufahrtregler in keinem prognostizierbaren oder gar linearen Verhältnis zu den tatsächlichen Motordrehzahlen stehen. Nur wenn aber die Drehzahlen exakt den Vorgaben entsprechen, bewegt sich der Katamaran in die gewünschte Richtung. Der Podwinkel lässt sich mit hinreichender Genauigkeit mit einem simplen Proportionalregler einstellen, da die Strecke selbst integrierend ist.
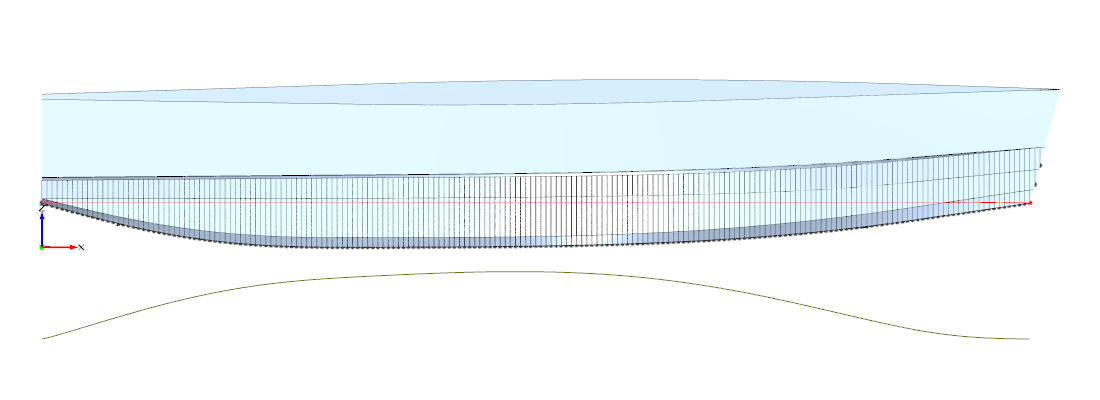
Die geregelten Werte werden nun an das Schiffsmodell übergeben, dass daraus Schiffsbewegungen berechnet. Das Schiffsmodell ist zwar stark vereinfacht, ist aber dennoch in der Lage, alle erforderlichen Schiffsbewegungen wiederzugeben. Abbildung 3 zeigt, dass ein nicht unwesentlicher Teil der Simulation in dem Schiffsmodell zu finden ist. Es würde aber den Rahmen dieser Seite sprengen, es im Detail zu erläutern.
In der Regelvariante werden der Drehwinkel $\alpha$ und die Winkelgeschwindigkeit $\omega$ des Katamarans im Rahmen einer Zustandsregelung zurückgeführt.
Simulationsergebnisse
Die Simulationsergebnisse zeigen, dass der Katamaran den Joystickbewegungen folgt, das Prinzip der Erzeugung eines beliebigen Schubvektors also funktioniert. Am Beispiel der Abbildungen 4 und 5 kann man gut erkennen, welchen Einfluss die Zustandsrückführung auf das Schiffsverhalten hat. Ein prinzipbedingtes Manko der reinen Vektorsteuerung ohne Drehwinkelfeedback ist, dass die reine Steuerung nicht die induzierte Drehbewegung des Schiffs modelliert, wenn sich dieses seitwärts bewegt. Der Grund dafür ist, dass in der Regel keine Daten eines Schiffs existieren, die eine Modellierung der seitlichen Bewegung erlauben würden. Dazu müsste man Werte berechnen, für Schiffsbewegungen von Vorausfahrt bis Rückwärtsfahrt und für alle Winkel (180°) dazwischen. Darüber hinaus können sich diese Werte bei meinem Katamaran mit Schwertern beliebig ändern, je nachdem wie weit die Schwerter gesteckt sind. Deshalb habe ich entschieden, diese induzierte Drehbewegung als Störgröße zu behandeln und separat auszuregeln.
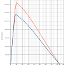
In Abbildung 4 lässt sich gut erkennen, dass der Drehwinkel (dicke schwarze Line) bei Seitwärtsfahrt kontinuierlich zunimmt. Im Vergleich dazu kann man in Abbildung 5 erkennen (ebenfalls die dicke schwarze Line), dass sich der Drehwinkel nach kurzer Einschwingzeit um die Null Grad herum einpendelt.
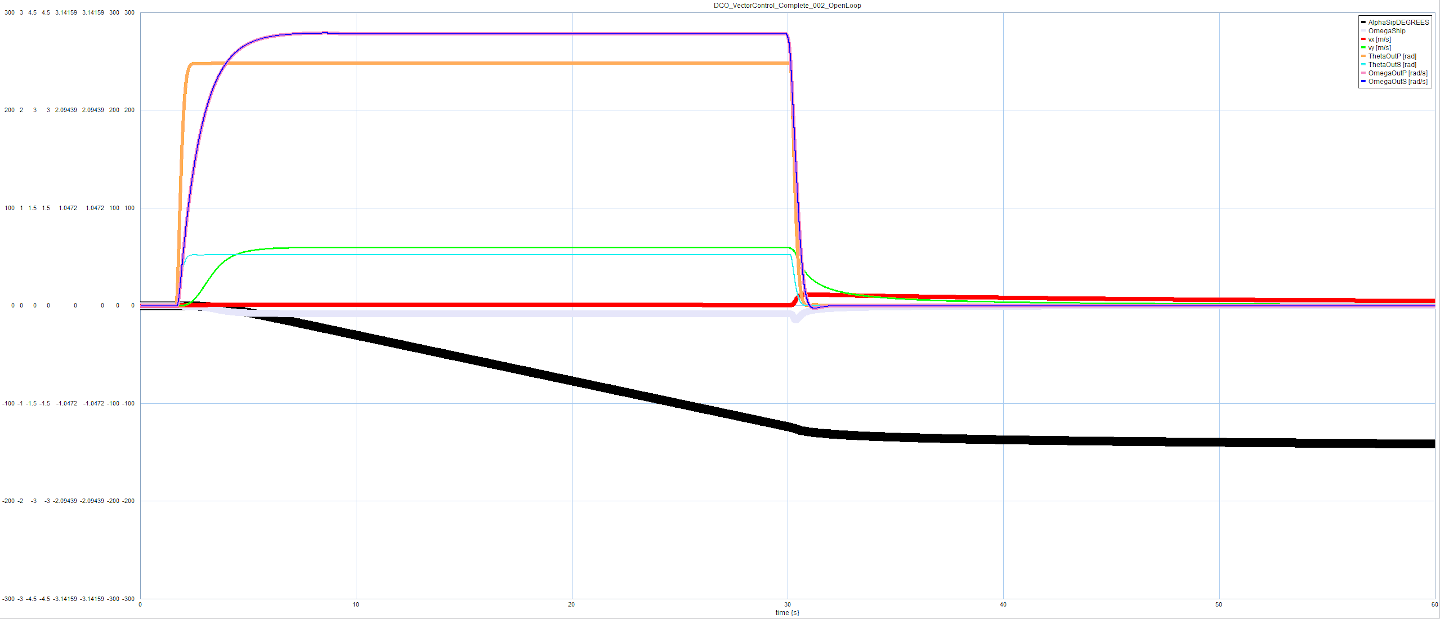
Abbildung 4: Open Loop Vektorsteuerung
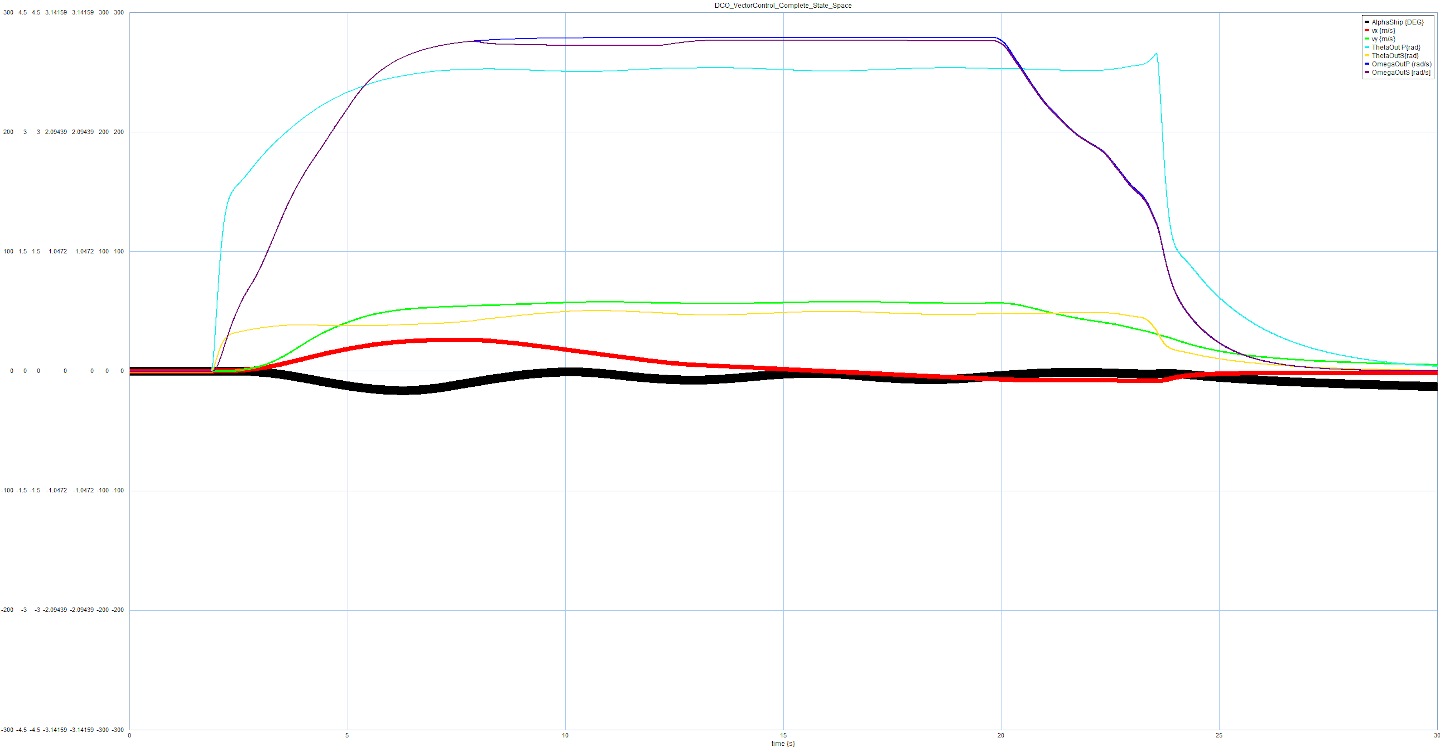
Abbildung 5: Closed Loop Vektorregelung

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998