03.05.2014
Wellenwiderstand im untersuchten Parameteraum (DoE 1)
Um ein Gefühl dafür zu bekommen, wie ein Design aussehen muss,
dass einen geringen Wellenwiderstand
aufweist, ist es sinnvoll, den
interessierenden Parameterraum systematisch abzusuchen. Dabei solle man vorher
verschiedene Dinge festlegen:
- Die zu variierenden Paramerter sind meistens mehr als man Rechenzeit hat. Ich habe mich daher auf die grundlegenden geometrischen Eigenschaften beschränkt: Maximalbreite (dBWLmax), Lage der Maximalbreite in Schiffslängsrichtung (dBWLmaxX), Breite am Heck (dBWLHeck), Tiefgang des Rumpfes ohne Anhhänge (dDraft (Tc)), Lage des maximalen Tiefgangs in Schiffslängsrichtung (dDraftX), Hauptspantfläche (SecA) und Lage der Hauptspantfläche in Schiffslängsrichtung (dSecAX). Macht zusammen sieben Parameter. Die Verdrängung, die Eintauchtiefe des Hecks, der Winkel der Bodenplatte (dead rise) und der Seitenplatten, Winkel des Überhangs am Bug, die Spitzheit am Bug etc. bleiben zunächst einmal konstant.
- Die Wertebereiche der Parameter wurden so bestimmt, dass möglichst viele Designs im
gültigen, d.h. in dem von dem Modell darstellbaren Bereich liegen.
Hier wurden 3072 Parameterkombinationen zu Grunde geleget.
2182 Kombinationen davon führten zu validen Modellen, von denen sechs
Modelle bei der Berechnung mit SHIPFLOW versagten. Die Werte im Einzelnen:
- dDraft: -0.95,-1.1:4 (alle 5cm)
- dDraftX: 9,12:4 (jeden Meter)
- dBWLmax: 0.8,0.9:3 (alle 5 cm, halbe Breite)
- dBwLmaxX: 9,12:4 (jeden Meter)
- dBWLrear: 0.6,0.75:4 (alle 5 cm, halbe Breite)
- dSecAX: 9,12:4 (jeden Meter)
- Man muss festlegen, was den
geringen Wellenwiderstand
definiert. Die Überlegung dabei ist, dass der Katamaran ein Fahrtenschiff für weltweite Fahrt werden soll. Dabei kommt es nicht so sehr auf mögliche erreichbare Spitzengeschwindigkeiten in Gleitfahrt an, sondern darauf, dass eine Reisegeschwindigkeit von 10 Knoten auch bei den überwiegend vorherrschenden leichten Winden erreicht werden kann. Dabei zeigt es sich, dass die Wellenwiderstandskurve bei einer Froudzahl von etwa $F_n=0.28...0.32$ ein relatives Maximum aufweist. Bei einer Wasserlinienlänge von ca. 20m entspricht dies einer Geschwindigkeit von 8,7 Knoten. Oberstes Ziel sollte es folglich sein, dieses Maximum so gering wie möglich zu halten, damit dieserWiderstandsberg
überwunden werden kann. Die Wellentheorie besagt, dass dies mit Hilfe der von mir gewählten Parameter möglich sein sollte. Allerdings soll dabei die Gleiteigenschaft auch nicht ganz aus den Augen gelassen werden. Daher wurde als zusätzlicher Wert noch $F_n=0.44$ bestimmt, der die Rumpfgeschwindigkeit markiert und als Maß dafür angesehen werden kann, wie leicht die Rumpfgeschwindigkeit überschritten werden kann, also die (Halb-)Gleitfahrt erreicht wird. Voruntersuchungen haben ergeben, dass bei Berechnung von $F_n=0.28, 0.30, 0.32, 0.44$ für alle 2182 Designs mein Rechner für die 8728 Berechnungen etwa 42 Tage (x24 Stunden!) benötigen würde. Dies hat sich in der Praxis bestätigt. - Als Letztes benötigen wir noch ein Referenzdesign mit dem die Ergebnisse verglichen werden können. Da ich kein vergleichbares reales Design habe, habe ich all meine Intuition, was ein gutes Modell ausmachen würde, zusammengenommen und habe mir aus den 2182 Designs das herausgesucht, was diesen Anforderungen am besten gerecht wird und habe dies als Referenzdesign definiert (Design_1745). Das Ganze stellt also auch einen Test meiner Intuition dar oder anders ausgedrückt, einen Test, wie weit man ohne CFD-Rechnungen kommen kann.
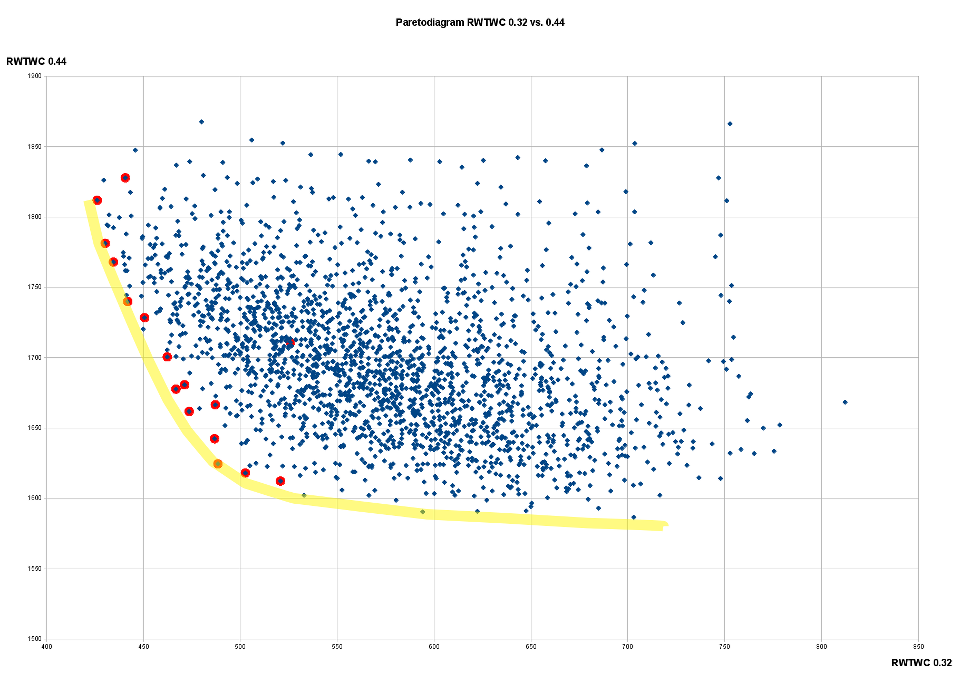
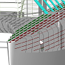
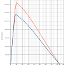
Abbildung 1: Paretodiagramm zur Modellauswahl
Zwei Designs sind nur dann unmittelbar vergleichbar, wenn sie auch dieselbe Verdrängung haben. Daher wurde die Hauptspantfläche dSecA in einem ersten Optimierungsschritt so mit Hilfe einer Brent-Optimierung angepasst, dass die Verdrängung im zehntel Promillebereich gleich ist, um jeden Einfluss auf die späteren Wellenwiderstandsberechnungen zu vermeiden. Da sich die zu optimierende Größe, also die Verdrängung, sprunghaft ändern kann, wenn das Design nicht mehr funktioniert, kam nur eine solche "suchende" Optimierung in Frage. Als Ergebnis kamen die Besagten 2182 Parametersätze heraus. Diese wurden in eine Tabelle exportiert. Diese Tabelle wurde in Teiltabellen von je 200 Designs zerlegt, um bei einem Absturz keine Totalverlste zu erleiden.
Für jede 200 Designs wurde eine eigene Datei im Friendship-Framework angelegt. Dort werden die Parametertabellen eingelesen. Anschließen wird ein Frienship-Script generiert, das für jedes Design eine EnsemleInvesitgation in Friendship erzeugt und damit die Berechnungen in SHIPFLOW ausführt.
Bei der Simulation kam es zu Problemen: Immer wider lieferte SHIPFLOW keine Werte für einzelne Designs oder blieb einfach hängen. Nach zwei Wochen inensiver Suche stellte sich heraus, dass die Wahl von abwickelbaren Flächen für Simulationen keine gute Wahl ist: Nur leicht verschränkte Platten führten dazu, dass die Sektionen, die in im Framework als Input für SHIPFLOW generiert werden, innerhalb einzelner Sektionen zusätzliche Anfangspunkte enthielten. SHIPFLOW kommt damit nicht klar. Dort dürfen die Sektionen nur genau einen Anfangspunkt haben, der auf der Symmetriebene liegt (normalerweise y=0). Daher wurden die abwickelbaren Flächen in einfache "ruled surfaces" umgewandelt und alle Probleme verschwanden.
Schließlich samelte ein ein weiteres Feature alle Werte aus den ResultTables so zusammen, das jedes Design eine Zeile in einer neu erzeugten Exceltabelle (genauer: Libreoffice Calc) bekommt.
Die Auswertung der Ergebnisse hat ergeben, dass "die Wahrheit", also gute Designs wohl im Bereich von Tc=0.95m bis Tc=1.00m liegen. Darüber hinaus scheint ein LB von ca. 11-11.5 günstig zu sein, was Maximalbreiten von etwa BWLmax=1.75 bis 1.82m entspricht. Die Hauptspantfläche bewegt sich dann im Bereich von 1.4-1.42m². Die Lage von Hauptspantfläche und Maximalbreite scheinen leicht achterlich der Schiffsmitte zu liegen. Eine genauere Untersuchung dieses Wertebereichs bietet sich daher an.
Ich habe jetzt 16 Designs ausgewählt, von denen zwei besonders hervorstechen: Design_0036 und Design_1489. Ich habe zunächst versucht anhand der Tabelle die Design durch berechnete Kennwerte auszuwählen. Da waren interessanterweise schon die beiden besten Designs dabei. Um meine Wahl objektiv zu untermauern und um weitere Kandidaten zu identifizieren, habe ich zwei Paretodiagramme angelegt: Einmal die auf transversalem Wellenschnitt basierenden Wellenwiderstände für Fn=0.32 vs. Fn=0.44 und einmal den Fn=0.32-Wert gegenüber der benetzten Fläche. Beim ersten Diagramm kann man gut die typische Pareto-Hyperbel erkennen, beim zweiten natürlich nicht, weil der Wellenwiderstand nicht so stark von der benetzten Fläche abhängt (beim Gesamtwiderstand sähe das natürlich ganz anders aus). Das zweite Diagramm diente zur Abschätzung: Ein richtig gutes Design muss auch eine kleine benetzte Fäche haben. Da bei Fn=0.32 der Reibungswiderstand doppelt bis dreimal so groß ist wie der Wellenwiderstand, wirken sich auch schon kleine Veränderungen bei der Fläche sehr negativ aus. Aus 1.5-2% Flächenzuwachs werden dann ganz schnell 5% Gesamtwiderstandszuwachs, was die gesamte Wellenwiderstandsreduktion zunichte macht. Die Fläche zu reduzieren wäre daher auch eine gute Sache, aber mir fällt keine sinnvolle Methode ein, wie ich das systematisch machen könnte. Interessant wäre sicher ein Rundspantdesign zum Vergleich.
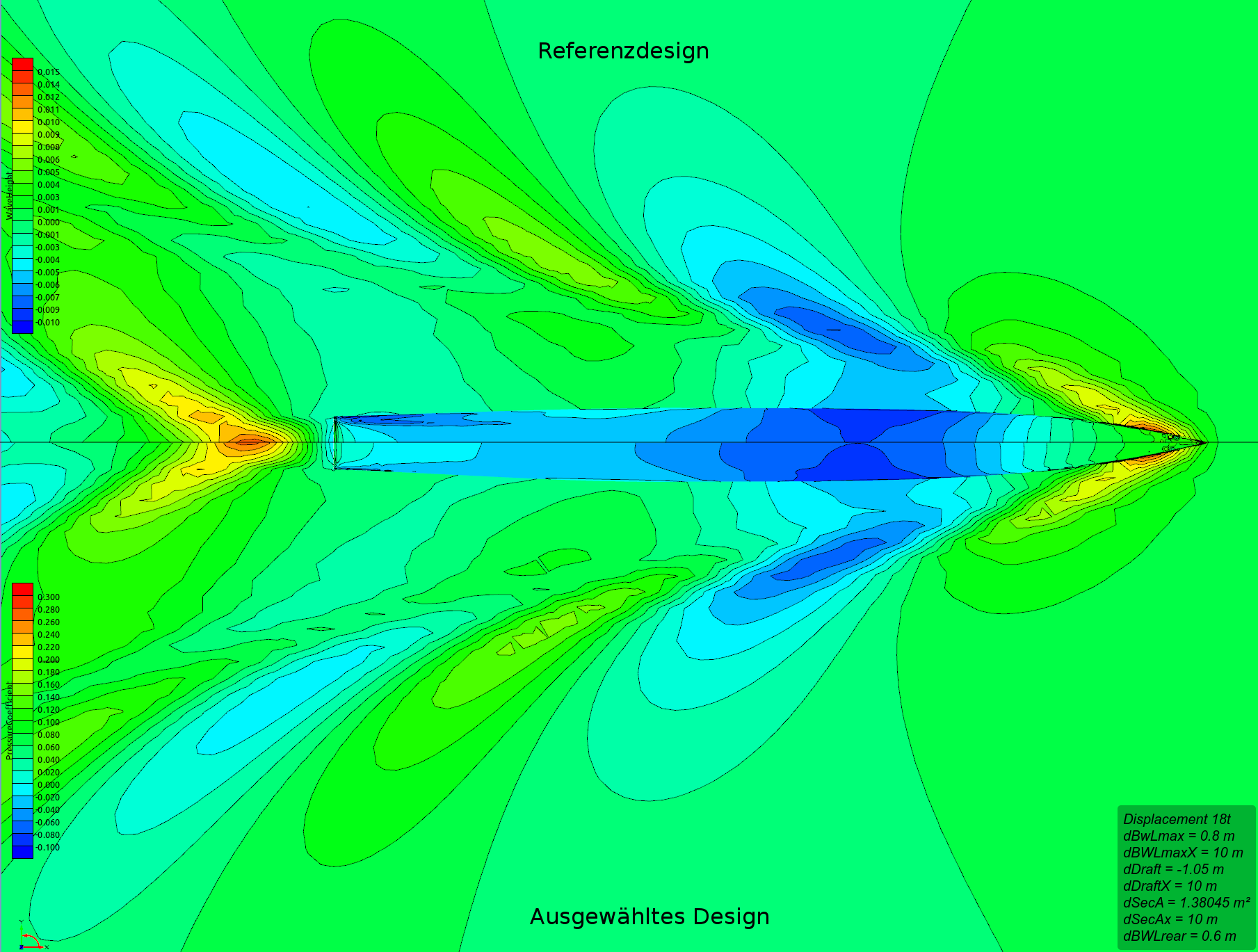
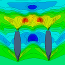
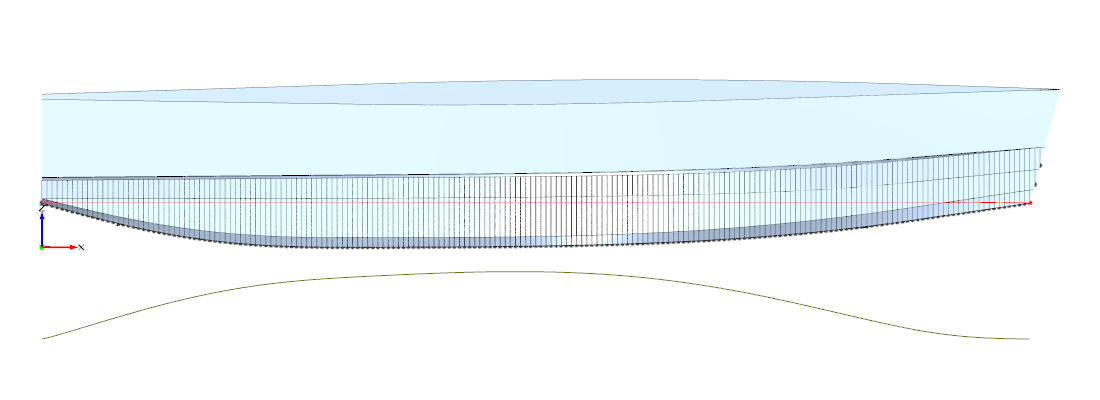
Abbildung 2: Wellenbildervergleich
Referenzdesign vs ausgewähltes Design
Beispielhaft ist hier ein Vergleich der Wellenbilder des Referenzdesigns zu einem der ausgewählten Designs abbgebildet (Abbildung 2). Es fällt auf, dass die Wellenhöhen des ausgewählten Designs etwas geringer sind. Auch die Druckverteilung am Rumpf zeigt weniger Unregelmäßigkeiten. Die Frage ist, ob letzteres nur auf eine zufällig bessere Diskretisierung zurückzuführen ist oder tatsächlich glattere Druckverteilungen widerspiegelt, was auf Lage und Geometrie der Knicke zurückgehen würde.
In einem weiteren Schritt wurde festgestellt, ob die ausgewählten Designs überhaupt baubar sind, d.h. die Daten wurden in das Modell mit den abwickelbaren Flächen zurückübertragen. Dabei fiel mir auf, dass ich in dem Design bei dem zweiten Knick (KnickP3_XY) aus mir nicht mehr nachvollziehbaren Gründen eine Anfangstangente am Heck vorgegeben hatte. Dies sollte sich bitter rächen: Bei stark überhöhter Darstellung der Kurvenkrümmung konnte man erkennen, dass alle Designs am Heck eine kaum wahrnehmbare Delle haben. Nachsimulationen der ausgewählten Designs ergaben, dass diese Delle einen erheblichen Einfluss auf den Wellenwiderstand bei $F_n=0.32$ hat. Somit sind leider alle Simulationen für die Mülltonne.
Aber jedes Schlechte hat auch sein Gutes: In den neuen Simulationen werde ich auf Grundlage der Ergebnisse einige Dinge verändern: Erstens werde ich nur die zwei Werte $F_n=0.32, 0.44$ berechnen. Das halbiert schon einmal die Rechenzeit. Außerdem werde ich die Parametergrenzen etwas ändern: Es fiel auf, dass alle guten Designs bei $BWL_{max}=1.8m$ und $BWL_{heck}=1.2m$ "klebten". Somit wird der Parameterbereich für auf $BWL_{max}=1.6...1.9m$ und $BWL_{heck}=1.1...1.4m$ geändert. Die Längslage der größten Breite bei $x=12m$ wurde ersatzlos gestrichen, weil der Wert keine sinnvollen Designs liefern konnte. Das wiederum führt dazu, dass es statt 3072 möglicher Designs nur 2304 geben kann. Auch davon werden sicher einige nicht gültig sein (die Modellparameterbestimmung läuft gerade), so dass ich bei wesentlich weniger als der halben Rechenzeit landen sollte, also vermutlich etwas 20 statt 42 Tage. Eigentlich hätte ich auch den Tiefgang von $T_c=1.1m$ streichen können, da dieser zusammen mit den gewählten Rumpfbreiten durchgängig zu kleine $BTR = {BWL_{max} \over T_c}$ (beam to draft ratio) Werte liefert (sollte etwa im Bereich 1.8...2.0 liegen).

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998