14.02.2013
CFD Berechnungen mit SHIPFLOW aus Sicht des Praktikers
Eine grundsätzliche Bemerkung kann ich mir an dieser Stelle nicht verkneifen: Ich finde es nicht angemessen, dass man sich die Randbedingungen und Grenzen einer Simulationssoftware wie SHIPFLOW aus einem Haufen wissenschaftlicher Veröffentlichungen und Dissertationen zusammensuchen muss. Bei einem kommerziellen Produkt wie SHIPFLOW erwarte ich, dass man mir diese Arbeit als Anwender abnimmt (sonst könnte ich auch OpenFOAM nehmen). Das zeigt, dass all diese Verfahren, dem reinen Wissenschaftsbetrieb noch kaum entkommen sind und immernoch kein Standard-Engineering-Werkzeug darstellen. Selbst ein Tutorial wie die Software zu benutzen ist, gibt es erst seit letztem Jahr (2012). Eine gewisse Vorsicht ist also geboten.
SHIPFLOW verwendet eine 2D-Panel-Methode (potential flow method) für den Wellenwiderstand und kombiniert diese mit einer viskosen Grenzschicht-Berechnung (boundary layer) an der Rumpfoberfläche, sowie einem RANS-Solver (Navier-Stokes-Solver) für den Heckbereich, um Viskositätseffekte (viscous resistance) zu bestimmen. Der Vorteil dieses Vorgehens liegt in reduzierter Rechenzeit (Janson1997E, Seite 6). Allerdings gibt es einen gravierenden Nachteil: Die RANS-Berechnung im Heckbereich wird auf Grundlage der Wellenform aus der 2D-Panelmethode durchgeführt. Die 2D-Methode ist jedoch ungenau bei der Berechnung der Heckwelle auf Grund von nicht berücksichtigten viskosen Effekten, die gerade im Heckbereich die Wellenform maßgeblich mitbestimmen, wenn es nicht eine glatte Abrisskante (Stichwort: dead water zone) gibt (Raven1996, Seite 195). Dies führt unter Umständen dazu, dass sich berechnete Widerstandsreduktionen für den Gesamtwiderstand nicht in der Praxis nachweisen lassen (Janson1997E, Zusammenfassung)
Flusspotentialmethode (Potential Flow Method) zur Wellenwiderstandsbestimmung
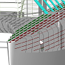
Die Netzgenerierung für die freie Wasseroberfläche wird durch die benötigte Rechenzeit einerseits und die erreichbare Genauigkeit andererseits bestimmt, d.h. das verwendete Netz sollte so grob wie möglich sein, ohne dabei große Diskretisierungsfehler zu machen.
Für lineare Wellenformberechnungen gilt das D'Alembert'sche Paradox. Dies besagt, dass wenn man den Schiffsrumpf an der glatten Wasseroberfläche spiegelt und dann die Druckverteilung um das Doppel-Modell (double model) integriert, dieses Integral Null sein muss. Leider gilt das für diskretisierte Rumpfformen nicht, aber der von Null abweichende Integralwert ist ein Indikator für die Güte des verwendeten Netzes und lässt sich darüber hinaus noch als Korrekturwert für die lineare Berechnung heranziehen.
Leider gilt das für nicht-lineare Berechnungen nicht. Allerdings scheinen die Diskretisierungsfehler auch für den nicht-linearen Fall geringer zu sein, wenn der Integralwert des Doppel-Modells kleiner ist (Janson1997E, Seite 9). Mit diesem Verfahren lässt sich also auch die Netzauflösung für den nicht-linearen Fall durch eine Netz-Sensitivitätsanalyse bestimmen.
Als Anhaltspunkt kann die Netz-Sensitivitätsanalyse von Jansen herhalten (Janson1997B, Seite 29ff.). Für die freie Oberfläche kann er in seinem Testfall ($Fn = 0,316$) eine Netzunabhängigkeit nachweisen, wenn er 30 Panele pro Wellenlänge in Schiffslängsrichtung verwendet und das erste Panel in Querrichtung nicht größer als $0,02 \cdot L_{pp}$ ist (vgl. Janson1997B, Seite 35, Tabelle 2). Für den Rumpf scheinen in seinem Fall 20 Panele in Längsrichtung und 5 in Querrichtung auszurechen, wenn er die Wellenformbetrachtet. Die numerischen Werte kommen ab einem Netz von 40x10 bis 40x15 zu einem relativen Stillstand (vgl. Janson1997B, Seite 31, Tabelle 1).
Heckpartien
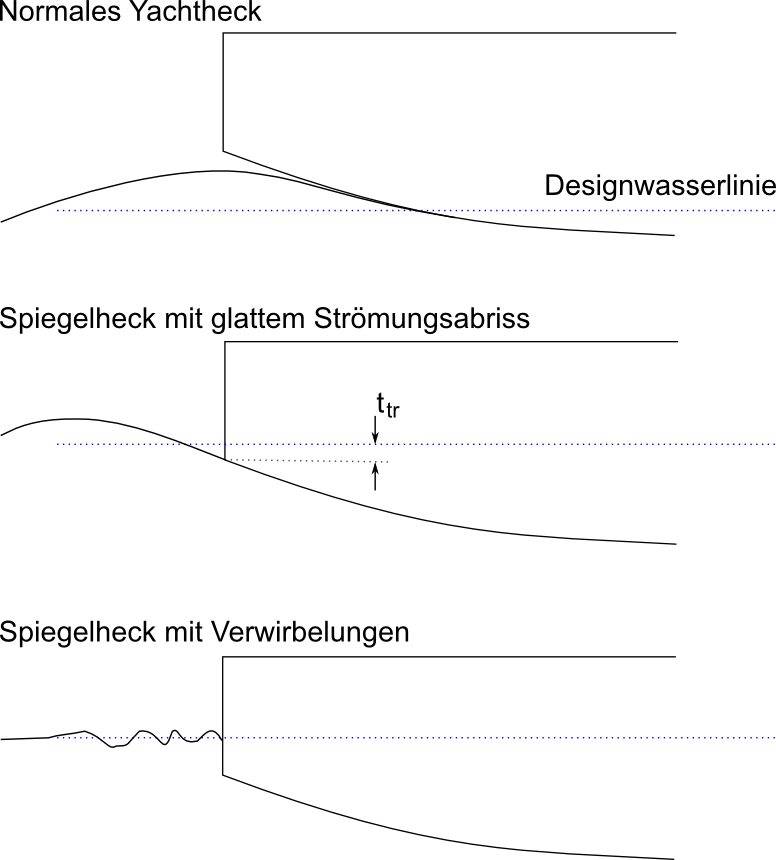
Verschiedene Heckpartien
Es müssen drei Heckpartien unterschieden werden (vgl. Raven1996, Seite 128):
- Normales Yachtheck mit Überhang (normal cruiser stern)
- Spiegelheck mit glattem Stömungsabriss an der Spiegelkante (dry transom stern)
- Spiegelheck mit Verwirbelungen hinter dem Spiegel (wet transom stern with dead water)
Fall 1 lässt sich mit einer nicht-linearen Flusspotentialmethode gut berechen, Fall 2 auch, wobei die Werte nur dann korrekt sind, wenn die Stömung tatsächlich glatt abreisst. Der dritte Fall (dead water) lässt sich grundsätzlich nicht mit einer Flusspotentialmethode berechen!
Leider kann man mit Hilfe der Flusspotentialmethoden die erforderliche Geschwindigkeit, bei der das Heck trocken fällt, nicht bestimmen. Man muss also Vorüberlegungen anstellen. Dabei ist die Froude-Zahl für Hecktauchtiefen $Fn_{tr}$ hilfreich. Sie ist in $\eqref{eq:Fntr}$ definiert. $$\begin{equation}Fn_{tr} = { V_s \over { \sqrt { - g \cdot t_{tr}}} } \label{eq:Fntr}\end{equation}$$ Dabei bezeichnet $t_{tr}$ die Spiegeltauchtiefe $[m]$ (negativer Wert, da unterhalb der Wasserlinie, die man bei $z = 0$ annimmt.), $g$ die Gravitationskonstante und $V_s$ die Geschwindigkeit des Schiffes $[m/s]$.
Wenn nun $Fn_{tr}$ größer ist als ein Grenzwert, fällt das Heck trocken. Dieser Grenzwert hat über die Jahre eine Entwicklung von ersten Schätzungen aus dem Jahre 1957 im Bereich $Fn_{tr} \approx 4..5$ bis hin zu experimentellen Ergebnisse von Maki et al. (Maki2004) im Bereich von $Fn_{tr} \approx 2$ entwickelt. Diese Werte liegen alle im Bereich des theoretisch Möglichen: Jansen führt aus, dass der theoretische Minimalwert für 2D-Betrachtungen bei $Fn_{tr} \approx 2,23$ liegt, für 3D-Betrachtungen bei $Fn_{tr} \approx 1,77$ (vgl. Jansen1996, Seite 148f.). Jansen führt aber auch aus, dass der tatsächliche Wert stark von der Form der Heckpartie abhängt und tendenziell eher zu einem "dead water" Bereich neigt. Also, wenn man nicht über einen 3D RANS Solver verfügt, muss man sich festlegen und hoffen, dass der Wert nicht komplett daneben liegt. Ich habe mich entschieden, bei einem $Fn_{tr} \approx 3..3,5$ von einem trockenen Spiegelheck auszugehen.
Quantitative Ergebnisse
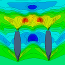
In der Literatur wird immer wieder betont, dass die Wellenbilder für das geübte Auge eines Fachmanns aussagekräftiger sind, als die berechneten Werte. Da mir leider dieses Fachwissen abgeht, bin ich auf die berechneten Werte angewiesen, zumal diese in der Regel ein recht zuverlässiges Ranking ermöglichen, auch wenn ihre Absolutwerte nicht exakt der Realität entsprechen.
Allerdings sagt Janson, dass Wellenschnitt-Widerstandsbeiwerte (wave cut resistance coefficient) in SHIPFLOW dichter an realen Messwerten liegen, als Werte, die man durch Integration der Druckwerte (pressure integration) bestimmt (vgl. Janson1997B, Zusammenfassung). Somit sollte man erstere zur Bewertung der Designs heranziehen.

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998