10.10.2015
Die Trapezregel im Segelmodell des ORC Int. VPP
Spätestens seit 2010 beruht die Flächenberechnung für das Großsegel des Segelmodells des dem VPP IMS/Orc Int. auf der Formel (1).
$A = {\frac {P}{8}} (E + 2 MGL + 2 MGM + 1,5 MGU + MGT + 0,5 HB)$ (1)

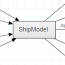
Abb. 1: Grossegelmaße
wobei die Größen wie in Abbildung 1 definiert sind. Im Klartext bedeuten sie:
| Bezeichner | Bedeutung |
|---|---|
| P | Vorlieklänge |
| E | Unterlieklänge |
| MGL | Großsegelbreite unten (Main Girth Lower) |
| MGM | Großsegelbreite mitte (Main Girth Middle) |
| MGU | Großsegelbreite oben (Main Girth Upper) |
| MGT | Großsegelbreite top (Main Girth Top) |
| HB | Großsegelkopfbrettbreite (Head Board) |
Numerische Flächenberechnung mit der Trapezregel
Allerdings dürfte wohl nur den wenigsten
Seglern klar sein, wie das ORC auf diese Formel gekommen ist. Dem werde ich im
Folgenden abhelfen. Desweiteren benötigt man für die Berechnung der Momente immer
den Flächenschwerpunkt der Segelgeometrie als Ausgangspunkt. In der
ORC VPP Documentation 2015
heißt es dazu nur lapidar The mainsail centre of
effort is calculated as the centre of the projected mainsail area, plus a constant
to unify the calculation with earlier equations
. Eine Formel
sparen sich die Kollegen an dieser Stelle lieber, denn wie sich unten zeigen
wird, lassen sich die dort gemachten Angaben nicht mit einer Anwendung der numerischen
Integration mittels Trapezregel in Einklang bringen. Da die Abweichung jedoch nur 1%
beträgt, werde ich die unten hergeleitete Formel dennoch verwenden.
Abbildung 1 zeigt darüber hinaus maßstabsgerecht die Main Sail Default Values
aus dem Jahre 2010 des IMS/ORC Int. für ein Rigg mit dem geometrischen
Breite-Höhenverhältnis von 1:3. Anhand der Abbildung 1 und mit Hilfe der Trapezregel
kann man die Gleichung (1) leicht herleiten. Die Trapezregel besagt, dass man eine
beliebige, kontinuierliche Kontur (am besten) in eine gerade
Zahl von gleich
großen Standintervallen $h$ unterteilt und für jedes Intervall die Teilfläche $a_i$ berechnet.
Um die eingeschlosse Gesamtfläche unter der Kontur zu berechnen, werden alle Teilflächen
einfach summiert, was gleichbedeutend mit einer numerischen Integration ist, also:
$A = {\displaystyle\int_0^P {ydx}} = {\displaystyle\sum_{i=1}^n a_i} \quad \text{wobei } \quad a_i = {\frac{y_{i-1}+y_i}{2}}h$ (2)
Die Teilflächen $a_i$ werden also aus den gemittelten $y$-Werten multipliziert mit der Standardintervallbreite $h$ berechnet. Berechnet man diese Summe zum Beispiel für n=4, kann man sie so umformen, dass jedes $y_i$ nur einmal auftaucht und mit einem individuellen Multiplikator multipliziert wird. Das Standardintervall $h$ wandert dabei vor die Summe:
$\begin{split}{{\displaystyle\sum_{i=1}^4 a_i}}& = a_1 + a_2 +a_3 +a_4 \\ &= {\frac{y_0+y_1}{2}}h + {\frac{y_1+y_2}{2}}h + {\frac{y_2+y_3}{2}}h + {\frac{y_3+y_4}{2}}h \\ & = h ({\frac{y_0}{2}} + y_1 + y_2 + y_3 + {\frac{y_4}{2}}) \end{split}$ (3)
Diese Formel läßt sich auf beliebige n erweitern, weil in diesem Fall lediglich in der Mitte weitere $y$-Werte mit dem Multiplikator 1 dazukommen. Nur an den Enden ist dieser Multiplikator $\frac{1}{2}$.
Einziger Knackpunkt: Das Standardintervall $h$ ist $\frac{P}{4}$, aber wegen der Rundung am Kopf wurde es dort verfeinert, indem das letzte Intervall in zwei $\frac{P}{8}$ Intervalle halbiert wurde. Der Grundansatz, die Teilflächen zu addieren, gilt aber auch hier, wobei bei den letzen zwei Summanden das halbierte Interval berücksichtigt werden muss:
$\begin{split}{{\displaystyle\sum a_i}}& = a_1 + a_2 +a_3 + a_{3.5} + a_4 \\ &= {\frac{y_0+y_1}{2}}h + {\frac{y_1+y_2}{2}}h + {\frac{y_2+y_3}{2}}h + {\frac{y_3+y_{3,5}}{2}}{\frac{h}{2}} + {\frac{y_{3,5}+y_4}{2}}{\frac{h}{2}} \\ & = {\frac{h}{2}} (y_0 + 2y_1 + 2y_2 + 1,5y_3 + y_{3,5} + 0,5y_4) \end{split}$ (4)
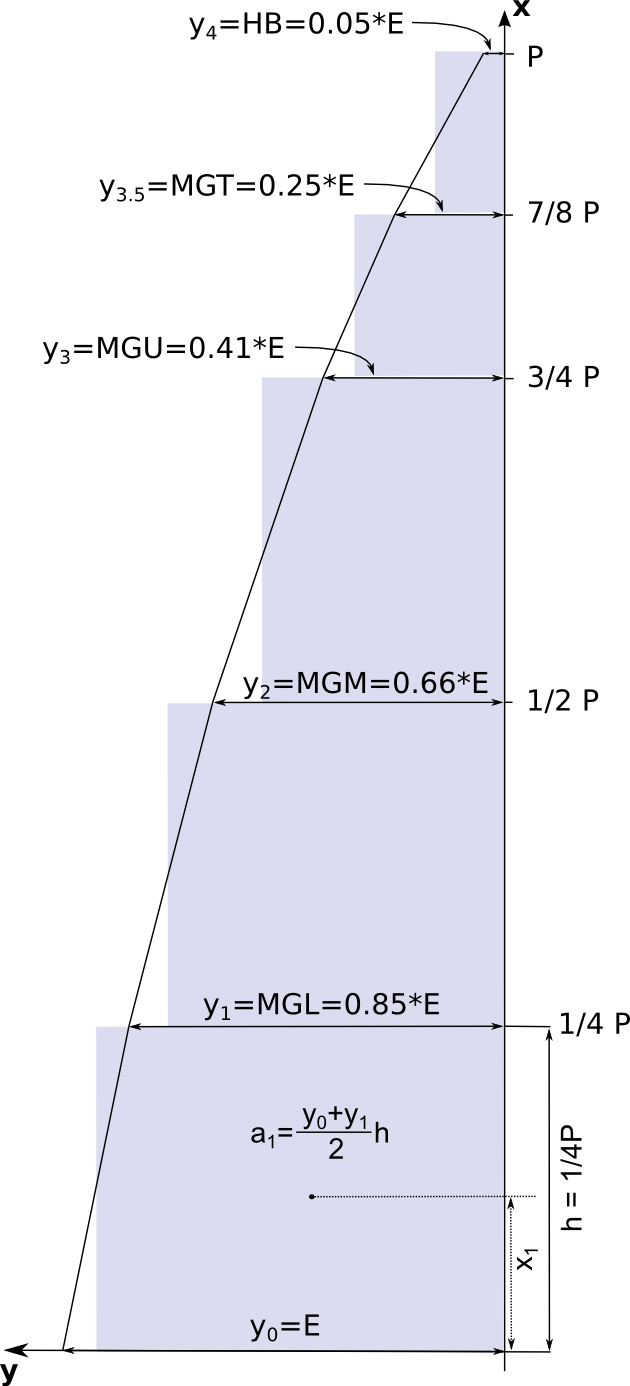
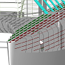
Abb. 2: $M_{yy}$ mathematisch
In Abbildung 1 sind die Flächen $a_1$, $a_2, $a_3$, $a_{3,5}$ und $a_4$ eingezeichnet. Ducrh die Umformung der Gleichung erhält man die gepunktet eingezeichneten Flächen. Da wir bei der Umrechnung keinen Fehler gemacht und keine zusätzlichen Annahmen getroffen haben, sind die bläulichen und die gestrichelten Flächen in Summe gleich. Mit etwas optischen Geschick sieht man auch das Problem der Trapezregel: Flächen unter konkaven Begrenzungslinien werden leicht unterschätzt.
Mit $h={\frac{P}{4}}$, $y_0=E$, $y_1=MGL$, $y_2=MGM$, $y_3=MGU$, $y_{3,5}=MGT$, $y_4=HB$ aus Abbildung 1 ergibt sich durch Einsetzen in Formel (4) unmittelbar Formel (1).
Numerische Berechnung des Flächenschwerpunkts mit der Trapezregel
Kommen wir nun dem Flächenschwerpunkt in $x$-Richtung, also in vertikaler Segelrichtung. Allgemein gilt, dass der Schwerpunkt in $x$-Richtung berechnet werden kann, indem man das Flächenmoment 1. Grades (auch statisches Moment, Einheit m³) um die $y$-Achse durch die Fläche dividiert, also:
$x^'= {\frac{M_{yy}}{A}} \qquad M_{yy} = {\displaystyle\int_0^P {xydx}} = {\displaystyle\sum_{i=1}^n x_ia_i} $ (5,6)
Aus Gleichung (6) ergibt sich, dass man zu numerischen Berechnung des statischen Moments, die einzelnen Teilflächen jeweils mit der Distanz ihres Flächenschwerpunktes multipliziert und anschließend alle summiert. Da die einzelnen Teilflächen bei der Trapezregel Rechtecke sind, liegt ihr Schwerpunkt ($x_i$) in der Intervallmitte wie in Abbildung 2 für das erste Intervall ($x_1$) dargestellt. Mathematisch korrekt gilt dann für unser Segel mit dem halbierten Intervall am Top:
$M_{yy}^M = {\displaystyle\sum_{i=1}^n x_ia_i} = x_1a_1 + x_2a_2 + x_3a_3 + x_{3,5}a_{3,5} + x_4a_4 $ (7)
Die $x_i$ lassen sich mit Hilfe der Intervallnummer $i$ als $x_i = (0,5 + (i-1))h$ ausdrücken, also für $i = 1$ ist der Hebelarm $x_1 = (0,5 + (1-1))h = 0,5h$. Dies und mit den $a_i$ aus der Flächenberechnung von oben eingesetzt in Gleichung (7)liefert:
$\begin{split}M_{yy}^M& = {\displaystyle\sum_{i=1}^n x_ia_i} \\ & = 0,5ha_1 + 1,5ha_2 + 2,5ha_3 + 3ha_{3,5} + 3,5ha_4 \\ & = 0,5h{\frac{y_0+y_1}{2}}h + 1,5{\frac{y_1+y_2}{2}}h + 2,5h{\frac{y_2+y_3}{2}}h + 3h{\frac{y_3+y_{3,5}}{2}}{\frac{h}{2}} + 3,5{\frac{y_{3,5}+y_4}{2}}{\frac{h}{2}} \end{split}$
Ausmultipliziert und zusammengefasst ergibt sich dann Gleichung (8), wobei die oben genannten Segelmaße (MGL, MGM, etc.) sich wie oben direkt einsetzen lassen:
$\begin{split}M_{yy} & = {\frac{h^2}{4}} (y_0 + 4y_1 + 8y_2 + 8y_3 + 6,5y_{3,5} + 3,5y_4) \\ & = {\frac {P^2}{4^2\cdot 4}} (E + 4 MGL + 8 MGM + 8 MGU + 6,5 MGT + 3,5 HB) \end{split}$ (8)
Gleichung (8) stellt die mathematisch und geometrisch konsequenteste Annäherung an das statische Moment dar. Im Schiffbau ist jedoch ein ganz simpler Ansatz üblich, der auf die manuellen Tage zurückgeht, in denen man solche Berechnungen von Hand in tabellarischer Form gemacht hat. In dieser Berechnung nimmt man einfach die schon aus der Flächenformel bekannte Umrechnung aus Gleichung (4) und gewichtet sie mit ihrem Hebelarm, der der $x$-Koordinate des zugehörigen $y$-Wertes entspricht, also für $y_0$ ist der Hebelarm Null, für $y_1$ ist der Hebelarm eine Intervallbreite $h$ usw. In einer Formel ausgedrückt bedeutet das im vorliegendan Fall:
$\begin{split}M_{yy}^S & = {\frac{h}{2}} (0 \cdot h y_0 + h \cdot 2y_1 + 2h \cdot 2y_2 + 3h \cdot 1,5y_3 + 3,5h \cdot y_{3,5} + 4h \cdot 0,5y_4) \\ & = {\frac{h^2}{2}} (2y_1 + 4y_2 + 4,5y_3 + 3,5y_{3,5} + 2y_4) \\ & = {\frac{h^2}{4}} (4y_1 + 8y_2 + 9y_3 + 7y_{3,5} + 4y_4) \\ & = {\frac {P^2}{4^2\cdot 4}} (4 MGL + 8 MGM + 9 MGU + 7 MGT + 4 HB) \end{split}$ (9)

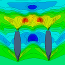
Abb. 3: $M_{yy}$ schiffbau
Abbildung 3 verschiebt die in Abbildung 1 durch Umrechnung erhaltenen (und in Gleichung (9) wieder verwendeten) gestrichelten Flächen in ihre zugehörigen Flächenschwerpunkte. Diese in Abbildung 3 nun violett-blau dargestellten Flächen bilden die Grundlage für die Berechnung in Gleichung (9). Ein Beispiel: Die Fläche um $x_1$ entspricht der Fläche $h \cdot y_1$, die dem zweiten Ausruck (der erste ins Null) in der ersten Zeile von Gleichung (9) entspricht, wenn man $\frac{h}{2}$ hineinmultipliziert. Der Hebelarm $x_1$ entspricht wie in Abbildung 3 zu sehen dem Intervall $h$. Ein Angriffspunktverschiebung ist hier nicht erforderlich. Durch den Intervallsprung bei $y_3$ ist dort eine Verschiebung erforderlich, so dass es zu einer Überlappung kommt.
Positiv fällt auf, dass den Einzelflächen ein mechanisch sinnvoller Hebelarm zugeordnet wird. Wie aber, wenn das erste Halbintervall vollkommen fehlt und sich durch die sub-Intervalle am Top die Flächen überlagern, daraus eine sinnvolle Momentenabschätzung werden kann, entzieht sich meiner Vorstellungskraft.
Abgleich Angriffsschwerpunktes mit ORC Int.
Die bereits zitierte Stelle aus der ORC VPP Documentation 2015
sagt weiter,
dass zu ddem durch Berechnung gewonnenen Wert $0,024 \cdot P$ addiert wird, um
eine Übereinstimung mit der Faustformel $x^'= 0,39P$ bei der Verwendung der
Standardsegelbreiten zu erreichen. Die Standardsegelbreiten sind als Teil der
Unterliekslänge definiert. Ich habe ich deshalb in
der Abbildung 1 bereits angegeben. Zur Überprüfung der Formeln habe ich ein mittelgroßen
Segel ausgewählt, mit $P = 12m$ und $E=4m$. Die Standardbreiten habe ich aus den
Minutes der ORC ITC (International Technical Committee) Sitzung
vom 29-31.10.2010 in Rom entnommen. Als mit den dort angegebenen Standardbreiten
ergeben sich dann:
$MGL = 0,85*E = 3,4m$
$MGM = 0,66*E = 2,64m$
$MGU = 0,41*E = 1,64m$
$MGT = 0,25*E = 1m$
$HB = 0,05*E = 0,2m$
Eingesetzt in Gleichung (1) erhält man eine Fläche von $A=29,46m^2$. Für den mathematische Ansatz erhält man für das Moment $M_{yy}^M = 132,84m^3$ (Gleichung (8)). Für den schiffbaulichen Ansatz erhält man für das Moment $M_{yy}^S = 128,88m^3$ (Gleichung (9)). Damit ergeben sich die Schwerpunkte zu$x^{'M}={\frac{M_{yy}^M}{A}} = 4,51m = 0,376P$
$x^{'S}={\frac{M_{yy}^S}{A}} = 4,375m = 0,365P$
Korrigiert um 0,024P ergibt sich $x_c^{'M}= 0,4P$ und $x_c^{'S}= 0,389P$. Es spricht also einiges dafür, dass der ORC den schiffbaulichen Ansatz wählt. Eine exakte Übereinstimmung gibt es jedoch nicht. Ob ich dem Folge, oder den etwas sichereren mathematischen Ansatz wähle, muss ich noch entscheiden.

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998