03.02.2016
Das aerodynamische Modell nach Hazen
Hier werde ich die wesentlichen Aspekte und Vorgehensweisen bei Hazens Modell beschreiben. Ich habe das Modell in einem CASES-Feature detailliert nachprogrammiert und kommentiert. Dort sollten alle noch so kleinen Details zu finden sein. Dazu die Datei einfach herunterladen, in das CASES-Feature-Verzeichnis schreiben, ein neues CAESES-Projekt anlegen und Feature laufen lassen.
| Auftriebskoeefizienten $(C_l)$ | Widerstandskoeefizienten $(C_{dp})$ | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Segel | 27 | 50 | 80 | 100 | 180 | 27 | 50 | 80 | 100 | 180 | ||
| Groß | 1,5 | 1,5 | 0,95 | 0,85 | 0 | 0,02 | 0,15 | 0,8 | 1,0 | 0,9 | ||
| Fock | 1,5 | 0,5 | 0,3 | 0 | 0 | 0,02 | 0,25 | 0,15 | 0 | 0 | ||
| Fock + 0,666 Spi | 1,5 | 1,499 | 0,966 | 0,5661 | 0 | 0,02 | 0,4165 | 0,7494 | 0,7992 | 0,43956 | ||
| Spinnaker | 0 | 1,5 | 1,0 | 0,85 | 0 | 0 | 0,25 | 0,9 | 1,2 | 0,66 | ||
| Besam | 1,3 | 1,4 | 1,0 | 0,8 | 0 | 0,02 | 0,15 | 0,75 | 1,0 | 0,8 | ||
| Besam-Vorsegel | 0 | 0,75 | 1,0 | 0,8 | 0 | 0 | 0,1 | 0,75 | 1,0 | 0 | ||
Das Modell wie Hazen es in der genannten Veröffentlichung beschreibt, geht von
Auftriebs- $(C_l)$ und parasitären Widerstandskoeffizienten $(C_{dp})$ für die
scheinbaren Windwinkel 27, 50, 80, 100 und 180 Grad aus (Tabellen 1 und 2).
Diese Werte sind nach Hazen Schätzungen für Großsegel, Fock, Spinnaker,
Besan und Besanvorsegel. Weniger bekannt ist, dass Hazen die Werte für die Fock
wie in der Tabelle angegeben anpasst, wenn die Spinnakerfläche gleich Null ist,
also kein Spinnaker gesetzt ist.
Auf Grundlage dieser Werte und der Geometrie der
tatsächlichen Segel bestimmt Hazen dann für jeden der fünf Angriffswinkel eine mit
jeweiligen Segelfläche gewichteten Summe für die Auftriebs- und
parasitären Widerstandskräfte, die dann durch Normierung auf die Normfläche
$A_{norm} = A_f + A_m + A_y$, wieder zu Beiwerten zurückgerechnet werden, wobei
die Indices f
für fore triangle
(Vorsegeldreieck), m
für main
(Großsegel) und y
für yawl
(Besam(haupt)segel) stehen.
Der Gesamtwiderstandsbeiwert besteht, wie oben bereits gesagt, zusätzlich zu dem
parasitären Widerstand $(C_{dp})$ noch aus dem induzierten Widerstandsbeiwert $C_{di}$.
Dieser setzt sich zusammen aus Segelendeffektbeiwert $K_{pp}$ und einem Wert, der
der auf dem Breiten-Höhen-Verhältnis (aspect ratio) beruht $K_{AR}$
Die letzten beiden Werte werden als ein efficency coefficient
$CE = K_{pp} + K_{AR}$ zusammengefasst. Dieser Wert mit $C_l^2$ multipliziert
ergibt den induzierten Widerstand, wie Hazen ihn definiert. Normalerweise wird
nur der Teil $K_{AR} \cdot C_l^2$ als induzierter Widerstand bezeichnet und
der Teil $K_{pp} \cdot C_l^2$ als quadratischer Profilwiderstand
(quadratic
profile drag). Schließlich wird noch der
Widerstandsbeiwert für den Rumpf und das Rigg auf Grundlage der einfachen
Formel nach Kerwin bestimmt. Diese bilden die Basisfür die von mir oben genannten
Kräfte der Aufbauten und des Riggs $(F_{{x/y}_r}^A, F_{{x/y}_m}^A, F_{{x/y}_v}^A)$.

Abbildung 1: Bezeichnungen nach Hazen
Das Resultat sind Vektoren von Beiwerten für die eingangs genannten Winkel. Als Hauptergebnis der Berechnungen stellt Hazen diese Werte dann als Spline-Kurven mit den Bezeichnungen CLM (maximaler Auftriebsbeiwert), CDM (maximaler (Gesamt-)widerstandsbeiwert, CDP (parasitärer Widerstandbeiwert), CE (Effizientfaktor), CDI (induzierter Widerstandsbeiwert) und CD0 (Widerstandbeiwert der Aufbauten) dar. In einer VPP-Berechnung bilden sie die Grundlage für die Segelkräfteberechnung.
Ist eine Besanbesegelung vorhanden, dann wirkt sich diese gemäß biplane theory
auftriebsbeiwerterhöhend und widerstandsbeiwertreduzierend auf die Besegelung des
Hauptmastes aus. Das hängt mit der geringern Verlangsamung der Strömung am Achterliek des
Großsegels zusammen. Dieser Effekt ist unter Seglern gemeinhin als Düseneffekt
zwischen Fock und Groß bekannt. Allerdings ist der Begriff Düseneffekt
eher
irreführend, weil er die physikalischen Zusammenhänge nicht treffend beschreibt.
Um einfacher rechnen zu können, schlägt Hazen diese Performazverbesserung allein
der Besanbegelung zu, wobei er den Effekt mit den Segelkräfteverhältnissen von
Hauptmastsegeln zu Besamsegeln skaliert.
In Formeln sieht das dann für den Auftriebsbeiwert so aus:
$\quad \text{(1)} \quad C_l[i]= \frac {C_{ls}[i]A_s+C_{lj}[i]A_j+C_{lm}[i]A_m+(C_{ly}[i]A_y+C_{lys}[i]A_{ys})\kappa[i]}{ A_{norm}} $
wobei die Laufvariable $i$ von 0 bis 4 läuft und die fünf Windangriffswinkel
27°, 50°, 80°, 100° und 180° abbildet. Der Index s
steht für Spinnaker.
Das $\kappa$ stellt den Multiplikator für die Auftriebsverbesserung durch die
Besambesegelung dar und berechnet sich zu:
$\quad \text{(2)} \quad \kappa[i]= \text{Fnkk}(Sig, Ngap)/Lratio$
Die Funktion $\text{Fnkk}(Sig, Ngap)$ wiederum bestimmt den Auftriebsverbesserungskoeffizienten basierend auf einer internen Tabelle, auf die unter Verwendung des Masthöhenverhältnisses von Besan- zu Hauptmast $Sig$ und dem einfallswinkelabhängigen Abstand zwischen den Masten $Ngap$ zugegriffen wird:
$\quad \text{(3)} \quad Sig = \frac { EHMaugy }{ EHMaug } \quad \quad \text{(4)} \quad Ngap = \frac {{2 \cdot EB \cdot sin(\beta[i])} }{ {Sumspan}}\quad$
wobei $Sumspan = EHMaug + EHMaugy$, die Summe der effektiven Masthöhen $(EHM)$ von Haupt- und Besanmast darstellen. In der $Ngap$-Formel wird durch den Mittelwert dieser Höhen geteilt, woraus sich die 2 im Zähler ergibt. Dabei ist im wesentlichen $EHMaug = max(IC, PC+BAD) + FBAV$ mit dem Durchschnittlichen Freibord $FBAV = 0,65 FF + 0,35 FA$. Analog gilt für den Besanmast $EHMaugy = PYC + FBAV$. Im wesentlichen deshalb, weil $EHMaug = PC + FBAV$ gilt, wenn keine Fock vorhanden ist $(IC = 0)$. Dies ist immer dann der Fall, wenn die Vorwindbesegelung bestehend aus Spi und Groß (und Besan, wenn vorhanden) berechnet wird. Die Am-Wind-Besegelung besteht definitionsgemäß aus Fock und Groß (und Besam, wenn vorhanden).
Der parasitäre Gesamtwiderstandsbeiwert des Riggs ergibt analog zur Auftriebsbeiwertformel nur, dass $\kappa$ hier keinen Einfluss hat, weil dieser Effekt dem induzierten Widerstandsbeiwert zugerechnet wird:
$\quad \text{(5)} \quad C_{dp}[i]= \frac { C_{dps}[i]A_s+C_{dpj}[i]A_j+C_{dpm}[i]A_m+C_{dpy}[i]A_y+C_{dpys}[i]A_{ys} }{ A_{norm}} $
Interessant ist die Bestimmung von $K_{pp}$ nach Hazen, wenn man das mit der aktuellen
Formel nach ORC 2015 vergleicht. Eigentlich sollte die Berechnung identisch sein, ist sie
aber nicht. Also, entweder ist die Formel in ORC 2015 falsch angegeben oder
Hazens Programm hat dort einen Fehler und zwar aus
folgenden Gründen: Bildet man die Formel [64] für den quadratic parasite drag
aus der ORC VPP Documentation 2015
auf die von Hazen benutzten Parameter ab, ergibt
sich:
$\quad \text{(6)} \quad K_{pp}[i] = \frac {K'' (C_{ls}^2[i]A_s+C_{lj}^2[i]A_j+C_{lm}^2[i]A_m+C_{ly}^2[i]A_y \kappa^2[i]+C_{lys}^2[i]A_{ys} \kappa^2[i])}{ A_{norm} C_l^2[i]} $
Mit $C_l[i]$ von oben ergibt sich:
$\quad \text{(7)} \quad K_{pp}[i] = \frac {K'' \cdot A_{norm} (C_{ls}^2[i]A_s+C_{lj}^2[i]A_j+C_{lm}^2[i]A_m+C_{ly}^2[i]A_y \kappa^2[i]+C_{lys}^2[i]A_ys \kappa^2[i])}{\lbrace C_{ls}[i]A_s+C_{lj}[i]A_j+C_{lm}[i]A_m+(C_{ly}[i]A_y+C_{lys}[i]A_{ys})\kappa[i]) \rbrace ^2} $
Hazen rechnet aber:
$\quad \text{(8)} \quad K_{pp}[i] = \frac {K'' \cdot A_{norm} (C_{ls}^2[i]A_s+C_{lj}^2[i]A_j+C_{lm}^2[i]A_m+C_{ly}^2[i]A_y \kappa^2[i]+C_{lys}^2[i]A_{ys} \kappa^2[i])} {(C_{ls}[i]A_s)^2+(C_{lj}[i]A_j)^2+(C_{lm}[i]A_m)^2+ \lbrace (C_{ly}[i]A_y)^2+(C_{lys}[i]A_{ys})^2 \rbrace \kappa^2[i]} $
Wie man bei genauem Hinsehen erkennen kann, sind die Nenner signifikant verschieden: Bei Hazen fehlen alle linear-gemischten Terme, weil Hazen das Quadrat nur auf die Einzelterme bezogen hat. Ich kann nicht mit 100%iger Sicherheit sagen, wer hier recht hat, allerdings erscheint mit die Formel nach ORC logischer.
Der aufmerksame Leser wird gemerkt haben, dass nun noch der Teil des induzierten Widerstandsbeiwert $C_{di}$ fehlt, der durch das Breiten-Höhen-Verhältnis (aspect ratio) definiert wird. Hazen spart sich da in seinem Programm ein paar Variablen, indem er diesen Wert gleich als $CE[i]$ ansetzt und später $K_{pp}[i]$ addiert, aber für die Darstellung ist es übersichtlicher, einen $K_{AR}$ separat zu definieren.
$\quad \text{(9)} \quad K_{AR}[i] = \frac {X[i]}{\pi \cdot AR \cdot E} \text{ mit } \bigg\lbrace \begin{smallmatrix} E = 1.1, AR = \frac{\text{max}(\text{EHMaug}^2 , \text{ EHMaugy}^2)}{A_{norm}} \text{ für } \beta=27°\\ E = 1.0, AR=\frac{\text{max}(\text{EHM}^2 , \text{ EHMy}^2)}{A_{norm}} \text{ für } \beta=50,80,100,180°\end{smallmatrix}$
Die $X[i] \leq 1$ sind Faktoren, die das Höhen-Breiten-Verhältnis des Riggs verbessern, wenn ein Besammast vorhanden ist und somit den induzierten Widerstand reduzieren. Sie beruhen genau wie die $\kappa[i]$ auf einer Funktion $\text{FnXi}(Sig, Ngap)$, die eine weitere Wertetabelle zur Grundlage hat.
Der induzierte Widerstand für den Winkel an der Vektorposition [i] $C_{di}[i]$ ergibt sich dann zu:
$\quad \text{(10)} \quad C_{di}[i] = (K_{pp}[i] + K_{AR}[i]) \cdot C_l^2[i]$
Die benutzten Segelflächen sind wie folgt definiert:
$\quad \begin{smallmatrix} \text{(11)} \quad A_m \quad = & 0,5 \cdot PC \cdot EC & \quad \text{(15)} \quad A_s \quad = & 0,75 \cdot 1,53 \cdot SL \cdot JC \\ \text{(12)} \quad A_j \quad \; = & 0,5 \cdot \sqrt{I^2+J^2} \cdot LP & \quad \text{(16)} \quad A_f \quad = & 0,5 \cdot IC \cdot J \\ \text{(13)} \quad A_y \quad \; = & 0,5 \cdot EYC \cdot PYC & \quad \text{(17)} \quad A_{ys} \quad = & \frac{YSD \cdot (2 \cdot YSMG + YSF)}{4} \\ \text{(14)} \quad A_{norm} \; = & A_f + A_m + A_y \end{smallmatrix}$
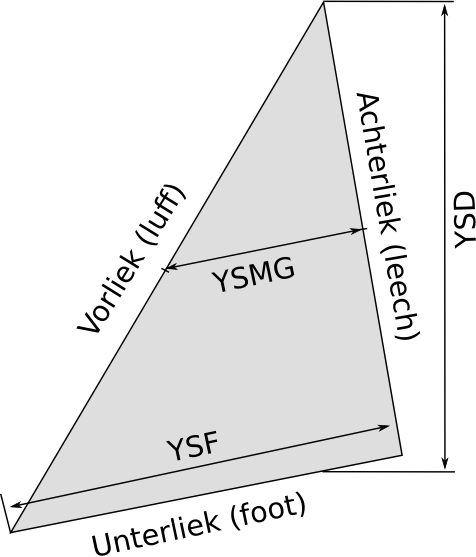
Abbildung 2: Besanvorsegel
Dabei ergeben sich die meisten Parameter aud Abbildung 1, also:
$PC$ = Vorlieklänge des Groß, $EC$ = Unterliekslänge des Groß,
$SL$ = Achterliekslänge des Spi (S wie Spi und L wie Leech), $IC$ = Achterliekslänge der
Vorsegeldreicks, $JC$ = Unterliekslänge des Vorsegeldreiecks. $LP$ = longest
perpendicular
, rechtwinkelig
gemessene Länge des größten Vorsegels (normalerweise die Genua),
$A_f$ das Vorsegeldreieck,
$EYC$ und $PYC$ analog die Vor- und Unterliekslängen des Besam(haupt)segels.
$YSF$, $YSMG$ und $YSD$ beziehen sich auf das Besamvorsegel und sind der Übersichlichkeit
halber in Abbildung 1 nicht dargestellt. Deshalb in Abbildung 2 eine Skizze.
$YSF$ steht für mzzen staysail foot
(Besamvorsegelunterliek, am Segel entlang gemessen),
$YSMG$ für mizzen staysail mid girth
(Breite des Besamvorsegels zwischen Vorliekmittelpunkt und Achterliekmittelpunkt) und
$YSD$ für mizzen staisail depth
(kürzeste Entfernung zwischen Segelkopf und Unterliek).
Das Programm
Das von Hazen veröffentlichte Programm berechnet die Auftriebs- und Widerstandskoeffizienten für die angegebenen Winkel (27,50,80, 100 und 180°) und stellt sie graphisch dar. Das von mir in CAESES nachprogrammierte Feature tut dies auch. Darüber hinaus liefert es drei Tabellen mit Vortriebs- und Krängungskräften sowie den wichtigsten berechneten Größen im Projektverzeichnis des CAESES-Projektes.
Die berechneten Werte für Cl, Cd, Cd0, Cdp und Cdi stimmen soweit eine Überprüfung anhand der von Hazen veröffentlichten Kurven möglich ist, überein. Darüber hinaus berechnet das Programm noch einen korrigierten Wert für Cdi. Die Korrektur beruht auf dem oben beschriebenen vermutlichen Fehler in Hazens Berechnung. Die Abweichung ist aber gering.
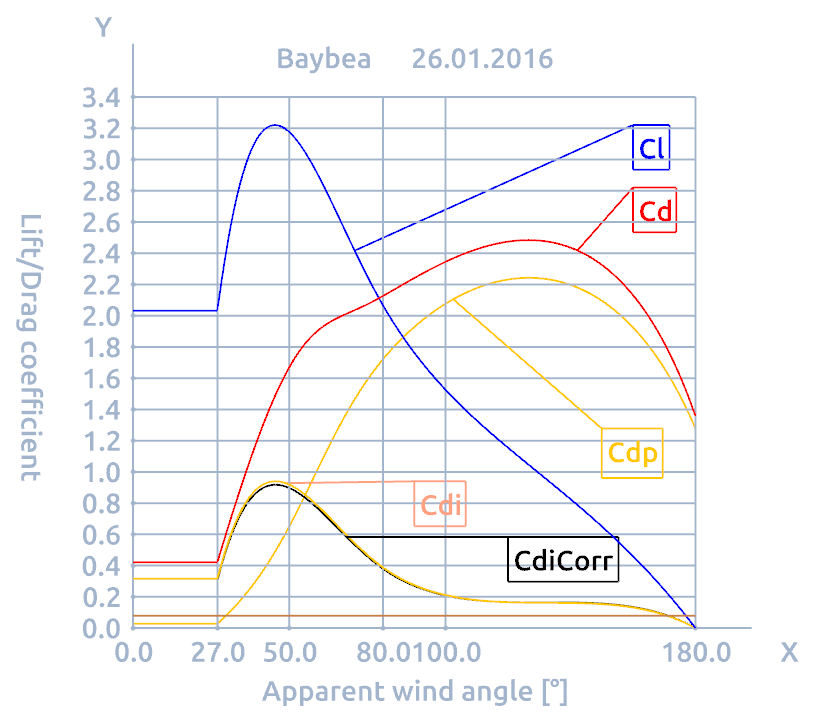
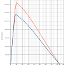
Abbildung 3: BayBea
Die Form der Kurven entspricht nicht exakt denen von Hazen. Es war mir nicht möglich
herauszufinden, welche Art von Spline-Interpolation Hazen dazu benutzt hat, weil dieser
Programmteil nicht abgedruckt ist. Trotz mehrfacher Versuche mit verschiedenen Splines
aus dem Vorrat von CAESES, konnte ich keine Übereinstimmung erzielen. Deshalb verwende
ich jetzt eine InterpolationCurve
mit Standardparametern. Es ist zu beachten,
dass die Gesamtwiderstandskoeffizentenkurve Cd aus der graphischen Addition
der Kurven Cd0, Cdp und Cdi entsteht, nicht aus der Interpolation der
Summenwerte für die einzelnen Winkel, durch die dann eine Splinekurve zu legen wäre.
Die Kurve $C{dp0}$ ist in der Grafik nicht gekennzeichnet. Die ist die orangefarbene
Gerade knapp über und parallel zu der $x$-Achse.
Somit ergibt sich der der Gesamtwiderstandsbeiwert in der Nomenklatur, die Hazen in seinem Programm verwendet zu:
$\quad \text{(18)} \quad C_d = C_{d0} + C_{dp} + C_{di}$, wobei
$\quad \text{(19)} \quad C_{d0} = 1.13* \frac {FBAV \cdot MHSB + EDMC \cdot EHM + EDMY \cdot EHMY}{A_{norm}}$
den Widerstandsbeiwert von Rumpf und Masten beschreibt. Dabei sind MHSB die Maximalbreite des Rumpfes, EDMC/EDMY ein durchschnittlicher Durchmesser von Haupt- und Besammast und EHM/EHMY die zugehörigen Masthöhen.
BayBea
Das Testmodell von Hazen war die BayBea. Der Graph für dieses Schiff ist in Abbildung 3 zu sehen. Jeder, der sich schon mal mit Auftriebs- und Widerstandskoeffizienten von Segeln beschäftigt hat, wird sich wundern, wie Hazens Modell hier auf eine $C_l \approx 3.2$ kommt. Dies hängt mit seiner Normierung zusammen: Er normiert auf Groß- und Vorsegeldreieck. BayBea hat aber eine riesige Genua, so dass diese Fläche als Vergrößerung von $C_l$ durchschlägt. Im Ganzen also nicht sehr realistisch, aber bei Hazen ging es wohl auch eher darum, die Idee der Einzelsegelbetrachtung zu etablieren.
Anmerkungen
Es gibt sehr viele Veröffentlichungen, die ein
Segelmodell nach Hazen
entweder beschreiben oder vorgeben zu benutzen. Diese
sehen oft etwas anders aus. Dies liegt in der Regel daran, dass man sich an dem
IMS-VPP-Modell nach Poor (poor1986 oder poor1990) orientiert, das auch das Segelmodell
von Hazen in leicht modifizierter Version verwendet oder aber daran, dass einer mal
geglaubt hat, etwas ganz Intelligentes zu schreiben und alle anderen nur
davon abgeschrieben haben, ohne die Quellen zu prüfen. Meine Beschreibung
beruht jedenfalls auf dem Original BASIC-Programmvon Hazen (hazen1980).
Besonders hartnäckig hält sich eine Angabe in der Literatur, wie denn die
aspect ratio
bei Hazen berechnet würde: Unter anderem in Larsson, Eliasson Principles of Yacht
Design
(larson2007), aber auch in anderen, wird folgendes geschrieben:
$\quad \text{(20)} \quad AR = \frac{(1.1 \cdot (\text{EHM +FBAV}))^2}{A_{norm}} \text{ für } \beta=27°$ $\quad \text{(21)} \quad AR = \frac{(1.1 \cdot \text{EHM})^2 }{A_{norm}} \text{ für } \beta=50,80,100,180°$
Bringt man die Angabe der programmierten Variante von oben auf ein vergleichbares Format, ergibt sich:
$\quad \text{(22)} \qquad AR = \frac{1.1 \cdot (\text{EHM +FBAV})^2}{A_{norm}} \text{ für } \beta=27°$ $\quad \text{(23)} \qquad AR=\frac{1.0 \cdot \text{EHM}^2 }{A_{norm}} \text{ für } \beta=50,80,100,180°$
Beide Formeln sind augenscheinlich alles anderes als gleich. In seinem Text beschreibt Hazen die Formeln so, wie in der Literatur oft verwendet, so programmiert sind sie aber nicht! Also entweder kann Hazen lausig beschreiben oder lausig programmieren... Ich persönlich halte die programmierte Variante für stichhaltiger:
- Einen Korrekturfaktor in der Formel zu quadrieren, ist ziemlich unsinnig. Man würde einfach das Quadrat als Korrekturfaktor wählen, also 1,21 in diesem Fall.
- Betrachtet man die physikalische Idee hinter dieser Korrektur, nämlich, dass sie einen gewissen Endplatteneffekt erfassen soll (bei einem fest mit einer Platte verbundenen Profil würde sich AR verdoppeln), erscheint es wenig sinnvoll davon auszugehen, dass dieser Effekt auch bei aufgefiertem Segel auftritt. Somit erscheint es richtig, dass sowohl der Faktor 1.1 also auch FBAV wegfallen.
Eine Anmerkung zu der Normierungsfläche $A_{norm}$ erscheint an dieser Stelle sinnvoll zu sein: Erstens ist die Frage zu klären: Wozu braucht er die überhaupt? Nun, zum einen deshalb, weil der auch die Widerstände von Rumpf und Rig auf eine einheitliche Fläche normieren muss, wenn er die Koeffizenten einfach addieren möchte. Trotzdem erscheint es fragwürdig, $C_{d0}$ dann auch mit der tatsächlichen Segelfläche zu multiplizieren, da dieser Widerstand ja unabhängig von der Segelfläche ist. Es ist nicht klar, wie Hazen das gemacht hätte, weil sein Programm ja keine VPP-Berechnung angibt. Es erscheint daher sinnvoll, $C_{d0}$ bzw. die sich daraus ergebenden Widerstandskräfte getrennt zu behandeln! Zum anderen benötigt man aber auch eine Bezugsfläche, wenn man in der VPP das Reffen einbeziehen möchte.
Und zweitens: Wie verwendet man $A_{norm}$ sinnvoll in einer VPP?
Für alle praktischen in meinem VPP werde ich mich daher an die ORC VPP Documentation
2015
(orc2015) anlehnen, wo die Rumpf und Rigangriffskräfte separat behandelt werden.
Darüber hinaus werde ich die Normierungsfläche auf die jeweils tatsächliche ungereffte
Fläche festlegen. Diese kann durchaus verschieden sein für verschiedene
Segelkombinationen und dient der Berechnung von $C_l$, $C_{dp}$ und $C_{di}$.
Über den Reffaktor erhält man dann Werte, die der Modellvorstellung eines gerefften
Segels entsprechen. Allerdings muss Cdi in jeder Iteration, in der sich der Refffaktor
ändert wegen der veränderten effektiven Masthöhe neu berechnet werden. Die Berechnung
ist also etwas komplizierter, als man vermuten würde.

-
2022
-
2021
-
2020
-
2019
-
2018
-
2017
-
2016
-
2015
-
2014
-
2013
-
2012
-
2011
-
2010
-
1998